Crude Oil Distillation Column
Crude oil distillation columns are essential for separating hydrocarbons into products with distinct boiling points, forming the backbone of petroleum refining processes. However, control of these columns is challenging due to nonlinearity, multi-component interactions, and disturbances in feed composition and flow rates. This study presents a high-fidelity model of a crude oil distillation column, incorporating detailed mass and energy balances, vapor-liquid equilibrium (VLE) relationships, and pressure variations along trays. Nonlinear Model Predictive Control (MPC) is applied to this model to optimize key operational parameters, including reflux ratio and reboiler duty. Simulation results demonstrate the effectiveness of the proposed controller in maintaining desired top and bottom compositions under disturbances. The study illustrates that high-fidelity modeling, paired with nonlinear MPC, improves control accuracy and robustness, offering practical insights into optimizing distillation processes.
Introduction
.Background and Motivation
Distillation columns play a critical role in petroleum refining, where crude oil is separated into various fractions, such as gasoline, diesel, and kerosene, based on boiling points. This process is highly energy-intensive, consuming about 40% of the energy in refining operations. Effective control of distillation columns is essential for maximizing product yield, improving efficiency, and reducing energy costs. However, distillation columns exhibit complex dynamics due to interactions among multiple components, nonlinear phase equilibria, and varying operational disturbances such as feed composition changes.
.Challenges in Distillation Control
Control challenges in crude oil distillation columns stem from their highly nonlinear nature and multivariable dependencies, including temperature, pressure, and flow rates along trays. Traditional control methods, such as Proportional-Integral-Derivative (PID) controllers, are limited in handling such complexity. Linear Model Predictive Control (MPC) offers improvements but often lacks the precision needed for crude oil applications due to linearization limitations. Nonlinear MPC, on the other hand, can account for process nonlinearity and provide accurate predictions and adaptive control in response to disturbances.
.Objectives and Contributions
This study aims to design a high-fidelity distillation column model for crude oil separation, incorporating detailed component interactions and dynamic changes across trays. By implementing nonlinear MPC using MODE, this research offers a framework for optimizing control of the reflux ratio and reboiler duty to achieve target compositions. Key contributions include:
- Development of a high-fidelity distillation model with component-specific mass and energy balances.
- Implementation of a nonlinear MPC controller for real-time optimization of control inputs.
- Validation of the controller’s ability to maintain composition targets under varying feed conditions.
Process Modeling
.Model Assumptions
To capture the key dynamics while maintaining computational feasibility, the following assumptions are made:
- Ideal mixtures are assumed for vapor-liquid equilibrium (VLE) calculations, using Raoult’s Law.
- Constant pressure drop across each tray, with a linear gradient from the top to the bottom.
- Thermal losses to the environment are neglected.
- Three components are considered: light, intermediate, and heavy, each with unique properties.
.Differential Equations for Mass and Energy Balances
The distillation model consists of differential equations representing component-wise mass balances and tray-level energy balances.
..Mass Balances
For each tray ![]() and component
and component ![]() , the mass balance is represented by:
, the mass balance is represented by:
(1) ![]()
where ![]() is the number of moles of component
is the number of moles of component ![]() on tray
on tray ![]() ,
, ![]() represents the feed,
represents the feed, ![]() and
and ![]() denote liquid and vapor flows respectively.
denote liquid and vapor flows respectively.
..Energy Balances
The energy balance on each tray ![]() is described by:
is described by:
(2) ![]()
where ![]() is the enthalpy on tray
is the enthalpy on tray ![]() represents heat input or output, and
represents heat input or output, and ![]() and
and ![]() are enthalpies entering and leaving the tray.
are enthalpies entering and leaving the tray.
.Vapor-Liquid Equilibrium and Thermodynamic Properties
The vapor-liquid equilibrium is calculated using Raoult’s Law:
(3) ![]()
where ![]() is the equilibrium constant,
is the equilibrium constant, ![]() is the heat of vaporization,
is the heat of vaporization, ![]() is the boiling point, and
is the boiling point, and ![]() is the universal gas constant. This model accounts for temperature and pressure variations along trays.
is the universal gas constant. This model accounts for temperature and pressure variations along trays.
Model Predictive Control Design
.Nonlinear MPC Structure
The nonlinear MPC framework in MODE is set with a prediction horizon of 20 steps and a control horizon of 5 steps, with a collocation-based discretization for differential states. The controller aims to optimize the operation by manipulating the reflux ratio ![]() and reboiler duty
and reboiler duty ![]() , ensuring product quality and energy efficiency.
, ensuring product quality and energy efficiency.
.Cost Function and Constraints
The objective function minimizes deviations from target compositions:
(4) 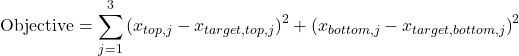
where ![]() and
and ![]() , are the compositions on the top and bottom trays, respectively. Constraints on control inputs include:
, are the compositions on the top and bottom trays, respectively. Constraints on control inputs include:
![]()
These bounds reflect typical operating limits in industrial distillation columns.
.Disturbance Rejection Strategy
To handle disturbances, the MPC model is periodically updated with observed feed compositions and rates. This ensures the controller remains responsive to fluctuations in feed quality and achieves robust performance.
Simulation and Results
.Setup and Initial Conditions
Simulations are conducted for a 10-tray distillation column with initial conditions set to achieve steady-state at specified feed compositions. The feed flow rate and composition are varied to introduce disturbances and evaluate the controller’s responsiveness.
.Analysis of Results
The nonlinear MPC effectively maintains desired top and bottom compositions under disturbances, with minimal oscillations. Results indicate:
- Dynamic Response: The controller rapidly adjusts reflux and reboiler duty, stabilizing composition profiles.
- Disturbance Handling: Step changes in feed composition result in temporary deviations, quickly corrected by MPC.
- Control Effort: The MPC controller optimally balances reflux ratio and reboiler duty, minimizing energy use.
Conclusion
This study demonstrates the value of high-fidelity modeling and nonlinear MPC for crude oil distillation control. By accurately modeling multi-component interactions and applying adaptive control, the proposed approach achieves robust composition control, even under disturbances. This framework provides a foundation for future work in real-time optimization and adaptive control in industrial distillation columns.
Future Work
Future studies can extend this model by incorporating real-time parameter estimation to update MPC models in real-world applications. Additionally, using advanced thermodynamic models like NRTL or UNIQUAC would allow for improved handling of non-ideal mixtures common in crude oil distillation.
