Reduction Cell
This paper introduces a model-based control strategy for optimizing the performance of a reduction cell in aluminum production, specifically through the management of energy and mass balances. The developed model includes energy transfer equations that capture the interactions between the bath, metal, and cell lining, as well as a detailed mass balance for key materials such as aluminum fluoride (AlF3). The control objective centers on regulating bath temperature, current efficiency, and material concentrations to enhance energy efficiency and reduce disturbances during operation. A predictive framework, built upon dynamic models, is employed to estimate three system states and two parameters, providing real-time control adjustments. This framework helps maintain temperature stability and minimizes the likelihood of anode effects, which can disrupt electrolysis. Simulations validate the proposed control strategy’s effectiveness in achieving stable and efficient process conditions.
Introduction
Aluminum production by electrolysis is an energy-intensive process where alumina (![]() ) is reduced in a cryolite bath (
) is reduced in a cryolite bath (![]() ) to produce aluminum. The high energy demands of the reduction process underscore the need for optimized cell performance, requiring precise control over energy inputs, heat losses, and chemical interactions within the electrolyte. Effective management of bath temperature, electrolyte composition, and current efficiency is essential to achieving process stability and minimizing energy wastage.
) to produce aluminum. The high energy demands of the reduction process underscore the need for optimized cell performance, requiring precise control over energy inputs, heat losses, and chemical interactions within the electrolyte. Effective management of bath temperature, electrolyte composition, and current efficiency is essential to achieving process stability and minimizing energy wastage.
This paper presents a model-based control approach designed to optimize the operational parameters of the reduction cell by using energy and mass balance equations. The model accounts for heat exchanges between the cell’s primary components—bath, metal, and lining—while tracking the dynamics of critical chemical inputs, such as aluminum fluoride (![]() ). Through the application of a predictive control framework, this approach regulates system inputs in real-time, balancing energy requirements against the need for stable production conditions. The control strategy not only aims to reduce energy losses but also maintains optimal bath conditions, thereby preventing process disruptions like anode effects and other efficiency-reducing incidents.
). Through the application of a predictive control framework, this approach regulates system inputs in real-time, balancing energy requirements against the need for stable production conditions. The control strategy not only aims to reduce energy losses but also maintains optimal bath conditions, thereby preventing process disruptions like anode effects and other efficiency-reducing incidents.
This research contributes to advancements in control strategies for aluminum reduction cells by proposing a predictive, model-based control framework that addresses the challenges of energy efficiency and process stability in high-energy industrial electrolysis applications.
System Modeling
In this section, we model the dynamics of the reduction cell, capturing its behavior through energy and mass balances. Key state variables include the bath temperature ![]() , electrolyte mass
, electrolyte mass ![]() , and the concentration of aluminum fluoride (
, and the concentration of aluminum fluoride (![]() ). The energy and mass balance equations describe how these quantities change over time, helping to maintain desired operating conditions.
). The energy and mass balance equations describe how these quantities change over time, helping to maintain desired operating conditions.
.Energy Balance on Bath, Metal, and Lining
The energy input into the reduction cell must account for the electrical energy supplied and the energy changes in the bath, metal, and cell lining, as well as energy losses. The balance equation is given by:
(1) 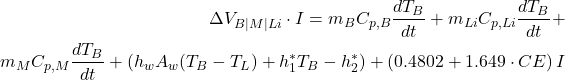
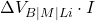 : Electrical input power, with
: Electrical input power, with 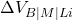 being the cell voltage across bath, metal, and lining, and
being the cell voltage across bath, metal, and lining, and 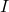 being the current.
being the current.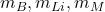 : Masses of the bath, lining, and metal respectively.
: Masses of the bath, lining, and metal respectively.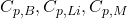 : Specific heat capacities of the bath, lining, and metal respectively.
: Specific heat capacities of the bath, lining, and metal respectively.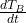 : Rate of temperature change of the bath.
: Rate of temperature change of the bath.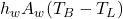 : Heat transfer between the bath and the lining through convection, where
: Heat transfer between the bath and the lining through convection, where 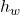 is the heat transfer coefficient and
is the heat transfer coefficient and 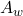 is the area.
is the area.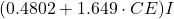 : Additional heat input related to the current and system configuration.
: Additional heat input related to the current and system configuration.
This balance ensures that the heat generated aligns with heat absorbed by the cell’s components and dissipated to its surroundings.
.Energy Balance on Ledge/Electrolyte Interface
At the interface between the solid ledge and the liquid electrolyte, heat transfer includes the energy involved in solidification and convective heat loss. The equation is:
(2) 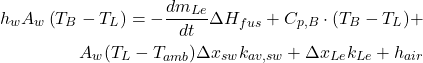
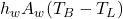 : Heat transfer between the bath and ledge.
: Heat transfer between the bath and ledge.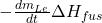 : Energy released as heat during the solidification of the electrolyte, where
: Energy released as heat during the solidification of the electrolyte, where 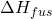 is the heat of fusion.
is the heat of fusion.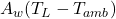 : Heat loss through the sidewall to ambient air.
: Heat loss through the sidewall to ambient air.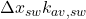 : Thermal conductivity across the sidewall.
: Thermal conductivity across the sidewall.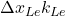 : Thermal conductivity of the ledge.
: Thermal conductivity of the ledge.
This balance ensures heat removal at the ledge-electrolyte interface, essential for maintaining operational temperatures and avoiding solidification issues.
.Mass Balance on 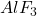
The mass dynamics of aluminum fluoride (![]() ) within the electrolyte are crucial for efficient electrolysis. This mass balance tracks
) within the electrolyte are crucial for efficient electrolysis. This mass balance tracks ![]() over time:
over time:
(3) ![]()
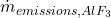 : Rate of aluminum fluoride emissions.
: Rate of aluminum fluoride emissions.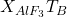 : Loss of
: Loss of 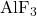 due to temperature effects in the bath.
due to temperature effects in the bath.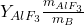 : Proportion of
: Proportion of 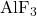 relative to the bath mass.
relative to the bath mass.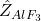 : External losses or additions.
: External losses or additions.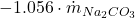 : Depletion of
: Depletion of 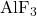 due to sodium carbonate addition.
due to sodium carbonate addition.
This equation manages the ![]() concentration to prevent excessive losses and maintain an optimal balance, avoiding detrimental effects like anode wear.
concentration to prevent excessive losses and maintain an optimal balance, avoiding detrimental effects like anode wear.
.Bath Mass Balance
The bath mass balance ensures that the mass of liquid and solid phases within the electrolyte remains consistent over time, reflecting system stability:
(4) ![]()
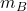 : Mass of the liquid bath.
: Mass of the liquid bath.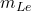 : Mass of the solid ledge.
: Mass of the solid ledge.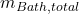 : Total mass of the bath.
: Total mass of the bath.
This equation simply ensures that any changes in the phases (liquid and solid) do not alter the total mass within the bath. Maintaining this balance is essential for efficient cell operation and stable electrolyte properties.
Control Strategy
The MPC framework is built around a dynamic model that continuously updates predictions for the reduction cell’s state variables. These predictions help in adjusting the system’s inputs in real time to maintain stability and energy efficiency. The primary objective is to regulate three key variables: current (I), voltage (ΔV), and the addition rate of ![]() . By controlling these, the framework maintains desired operational conditions, such as optimal bath temperature and appropriate levels of
. By controlling these, the framework maintains desired operational conditions, such as optimal bath temperature and appropriate levels of ![]() concentration in the electrolyte.
concentration in the electrolyte.
.System States
The system model tracks three primary states:
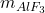 : This represents the mass of
: This represents the mass of 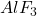 in the electrolyte (in kg). Accurate monitoring and control of
in the electrolyte (in kg). Accurate monitoring and control of 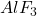 are critical, as it directly impacts the bath’s electrolyte composition, current efficiency, and overall stability of the reduction process.
are critical, as it directly impacts the bath’s electrolyte composition, current efficiency, and overall stability of the reduction process.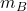 : This state indicates the mass of the liquid electrolyte (in kg), a critical variable as it contributes to bath stability and influences temperature dynamics.
: This state indicates the mass of the liquid electrolyte (in kg), a critical variable as it contributes to bath stability and influences temperature dynamics.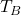 : The electrolyte temperature, which is central to the electrochemical process. Temperature control ensures efficient reactions without overheating, which could lead to unwanted energy losses or cell damage.
: The electrolyte temperature, which is central to the electrochemical process. Temperature control ensures efficient reactions without overheating, which could lead to unwanted energy losses or cell damage.
.Inputs and Outputs
In this control system, inputs directly influence system states, while outputs provide real-time feedback that is essential for adjusting inputs to maintain stability.
- Inputs:
- Cell Current (I): Adjustments in current directly affect the rate of electrochemical reactions, impacting the reduction process’s efficiency and stability.
- AlF₃ Addition Rate (
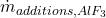 ): This rate (kg/s) manages
): This rate (kg/s) manages 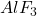 concentration, keeping it within the optimal range to prevent anode effects and ensure smooth operation.
concentration, keeping it within the optimal range to prevent anode effects and ensure smooth operation. - Cell Voltage (ΔV): Adjustments in voltage help control energy distribution within the cell, balancing energy input with heat loss.
- Outputs:
- Measured Bath Temperature (
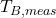 ): Real-time feedback on the bath temperature, crucial for making real-time adjustments in current or AlF₃ addition rates.
): Real-time feedback on the bath temperature, crucial for making real-time adjustments in current or AlF₃ addition rates. - Measured
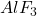 Concentration (
Concentration (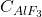 ): Indicates the percentage of
): Indicates the percentage of 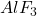 in the bath, helping prevent anode effects and ensure efficiency.
in the bath, helping prevent anode effects and ensure efficiency. - Measured Superheat (
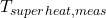 ): Superheat is the difference between the bath temperature and the melting point of the cryolite-alumina mixture, providing an indication of bath stability and reaction readiness.
): Superheat is the difference between the bath temperature and the melting point of the cryolite-alumina mixture, providing an indication of bath stability and reaction readiness.
- Measured Bath Temperature (
Results and Discussion
.Simulation Setup
The control model was implemented in a simulated environment where variables such as heat transfer coefficients (![]() ) were estimated using data from typical reduction cells. The initial setup represented baseline operating conditions, with stabilized bath temperature and target
) were estimated using data from typical reduction cells. The initial setup represented baseline operating conditions, with stabilized bath temperature and target ![]() concentration.
concentration.
.Performance Evaluation
The effectiveness of the model-based control strategy was evaluated across several performance metrics:
- Temperature Control: The system maintained the bath temperature within a narrow range, avoiding excessive fluctuations that could compromise the reduction process or increase energy costs.
- Aluminum Fluoride Management: The control framework successfully regulated the concentration of
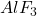 in the electrolyte, thus minimizing anode effects, reducing emissions, and ensuring consistent process conditions.
in the electrolyte, thus minimizing anode effects, reducing emissions, and ensuring consistent process conditions. - Energy Efficiency: By optimizing voltage and current inputs, the model achieved a balance between energy consumption and production efficiency, resulting in significant energy savings compared to traditional control methods.
Simulation outcomes indicate that the MPC framework enhanced both process stability and energy efficiency by dynamically adjusting inputs to respond to operational disturbances and minimize energy waste.
Conclusion
The model-based predictive control strategy proposed here provides a robust solution for managing aluminum reduction cells. By incorporating energy and mass balance equations, the approach maintains precise control over bath temperature, current efficiency, and AlF₃ concentration, ultimately leading to improved process stability and reduced energy costs. The predictive nature of the control system enables it to anticipate disturbances and adjust inputs proactively, which minimizes production downtime and optimizes resource usage.
Future Work: The next steps involve testing the model within an industrial setting, integrating real-time data for adaptive control, and further refining the predictive algorithms to handle variability in production demands.
