Small Modular Reactor – a model-based control approach
Small Modular Reactors (SMRs) are poised to revolutionize nuclear power generation through their enhanced safety and modularity. Effective control of SMRs is paramount for maintaining operational stability and safety under varying conditions. This paper presents a comprehensive control strategy for SMRs using Model Predictive Control (MPC), grounded in a differential equation framework. The reactor’s neutron dynamics are modelled using point kinetics equations, while a simplified lumped thermal model captures the reactor core temperature dynamics. The control input, reactivity ρ(t), represents various reactivity control methods. Through simulations, we demonstrate the effectiveness of the MPC strategy in maintaining desired operational parameters, optimizing performance, and responding to disturbances.
Introduction
The development of Small Modular Reactors (SMRs) marks a significant advancement in nuclear power technology, bringing with it a host of advantages that could transform the energy landscape. These advantages include reduced capital costs, enhanced safety features, and versatile deployment options that can adapt to various settings—rural areas, industrial sites, or integrated with renewable energy sources. Unlike traditional large reactors, SMRs offer a more flexible approach to nuclear energy, making them suitable for a broader range of applications.
As the nuclear power sector evolves, the complexity of managing these reactors has become increasingly apparent. The dynamics involved in SMRs are driven by intricate nuclear reactions and thermal-hydraulic processes, necessitating sophisticated control mechanisms to maintain operational stability and safety. The inherent challenges in controlling the behavior of SMRs lie in the intricate relationships between neutron density, thermal responses, and reactivity, making it essential to implement advanced control strategies that can effectively navigate these complexities.
.Problem Statement
Controlling the behavior of an SMR presents unique challenges that stem from the complexities of neutron dynamics and thermal responses. The interplay between these factors is nonlinear and often multivariable, leading to unpredictable behaviors that traditional control methods, such as Proportional-Integral-Derivative (PID) controllers, struggle to manage effectively. PID controllers, while useful in many industrial applications, are limited in their capacity to handle the dynamic and often non-linear characteristics of reactor operations. This limitation is particularly evident in scenarios where rapid changes occur, requiring swift adjustments in control actions.
Consequently, there is a growing necessity to explore advanced control strategies that can accommodate the multifaceted nature of SMR operations. Model Predictive Control (MPC) emerges as a compelling solution, offering the ability to predict future behavior based on current states while considering constraints and optimization objectives. MPC not only allows for more effective handling of the nonlinear dynamics of SMRs but also provides a framework for decision-making that enhances reactor performance and safety.
.Objectives
The primary objectives of this paper are structured to address the challenges posed by SMR dynamics and to leverage advanced control methodologies for improved reactor management:
Develop a Mathematical Model for Neutron Dynamics: This objective involves creating a robust mathematical representation of the neutron behavior within the reactor core, employing point kinetics equations alongside a simplified lumped thermal model to capture the thermal dynamics. This model will serve as the foundation for understanding how various parameters affect reactor stability and reactivity.
Formulate a Model Predictive Control (MPC) Strategy: Building upon the mathematical model developed, the second objective focuses on designing an MPC strategy tailored specifically for SMRs. This strategy will utilize the derived model to predict future states of the reactor, allowing for optimized control actions that ensure stability and responsiveness to operational changes.
Evaluate the Performance of the MPC through Simulation: The final objective entails conducting comprehensive simulations to assess the effectiveness of the MPC strategy in controlling reactivity and maintaining stability within the reactor. This evaluation will highlight the advantages of MPC over traditional control methods, demonstrating its potential to enhance operational safety and efficiency in SMRs.
Point Kinetics Model
The development of Small Modular Reactors (SMRs) marks a significant advancement in nuclear power technology, bringing with it a host of advantages that could transform the energy landscape. These advantages include reduced capital costs, enhanced safety features, and versatile deployment options that can adapt to various settings—rural areas, industrial sites, or integrated with renewable energy sources. Unlike traditional large reactors, SMRs offer a more flexible approach to nuclear energy, making them suitable for a broader range of applications.
As the nuclear power sector evolves, the complexity of managing these reactors has become increasingly apparent. The dynamics involved in SMRs are driven by intricate nuclear reactions and thermal-hydraulic processes, necessitating sophisticated control mechanisms to maintain operational stability and safety. The inherent challenges in controlling the behaviour of SMRs lie in the intricate relationships between neutron density, thermal responses, and reactivity, making it essential to implement advanced control strategies that can effectively navigate these complexities.
.Problem Statement
Controlling the behaviour of an SMR presents unique challenges that stem from the complexities of neutron dynamics and thermal responses. The interplay between these factors is nonlinear and often multivariable, leading to unpredictable behaviours that traditional control methods, such as Proportional-Integral-Derivative (PID) controllers, struggle to manage effectively. PID controllers, while useful in many industrial applications, are limited in their capacity to handle the dynamic and often non-linear characteristics of reactor operations. This limitation is particularly evident in scenarios where rapid changes occur, requiring swift adjustments in control actions.
Consequently, there is a growing necessity to explore advanced control strategies that can accommodate the multifaceted nature of SMR operations. Model Predictive Control (MPC) emerges as a compelling solution, offering the ability to predict future behavior based on current states while considering constraints and optimization objectives. MPC not only allows for more effective handling of the nonlinear dynamics of SMRs but also provides a framework for decision-making that enhances reactor performance and safety.
.Objectives
The primary objectives of this paper are structured to address the challenges posed by SMR dynamics and to leverage advanced control methodologies for improved reactor management:
Develop a Mathematical Model for Neutron Dynamics: This objective involves creating a robust mathematical representation of the neutron behaviour within the reactor core, employing point kinetics equations alongside a simplified lumped thermal model to capture the thermal dynamics. This model will serve as the foundation for understanding how various parameters affect reactor stability and reactivity.
Formulate a Model Predictive Control (MPC) Strategy: Building upon the mathematical model developed, the second objective focuses on designing an MPC strategy tailored specifically for SMRs. This strategy will utilize the derived model to predict future states of the reactor, allowing for optimized control actions that ensure stability and responsiveness to operational changes.
Evaluate the Performance of the MPC through Simulation: The final objective entails conducting comprehensive simulations to assess the effectiveness of the MPC strategy in controlling reactivity and maintaining stability within the reactor. This evaluation will highlight the advantages of MPC over traditional control methods, demonstrating its potential to enhance operational safety and efficiency in SMRs.
Point kinetics simplifies the complex spatial dynamics of neutron behaviour in a reactor core to a single point model. The core dynamics are primarily described by the following equations:
.Neutron Density
The neutron density ![]() changes over time according to the differential equation:
changes over time according to the differential equation:
(1) ![]()
Where:
– ![]() is the neutron density at time (t).
is the neutron density at time (t).
– ![]() is the prompt neutron generation time.
is the prompt neutron generation time.
– ![]() is the reactivity at time (t).
is the reactivity at time (t).
– ![]() is the fraction of delayed neutrons.
is the fraction of delayed neutrons.
– ![]() is the equilibrium neutron density.
is the equilibrium neutron density.
.Delayed Neutron Precursors
The delayed neutron precursor density ![]() for the
for the ![]() group is described by:
group is described by:
Where:
(2) ![]()
– ![]() is the density of delayed neutron precursors of group
is the density of delayed neutron precursors of group ![]() at time
at time ![]() .
.
– ![]() is the fraction of delayed neutrons produced by group
is the fraction of delayed neutrons produced by group ![]() .
.
– ![]() is the decay constant for group
is the decay constant for group ![]() .
.
The total neutron density ![]() can be represented as:
can be represented as:
(3) 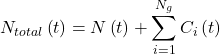
Where ![]() is the number of delayed neutron groups.
is the number of delayed neutron groups.
Thermal Dynamics Model
.Simplified Lumped Thermal Model
The thermal behaviour of the reactor core can be modelled using a lumped parameter approach. The core temperature ![]() evolves according to:
evolves according to:
(4) ![]()
Where:
– ![]() is the heat capacity of the reactor core.
is the heat capacity of the reactor core.
– ![]() is the power generated within the reactor.
is the power generated within the reactor.
– ![]() is the heat lost to the environment.
is the heat lost to the environment.
– ![]() is the heat removed by the cooling system.
is the heat removed by the cooling system.
The heat generation can be related to neutron density and reactivity as follows:
(5) ![]()
Where ![]() is a proportionality constant relating neutron activity to thermal power.
is a proportionality constant relating neutron activity to thermal power.
.Heat Loss and Cooling
The heat loss can typically be modelled as:
(6) ![]()
Where ![]() is the ambient temperature and
is the ambient temperature and ![]() is the heat transfer coefficient.
is the heat transfer coefficient.
The cooling term can be expressed as:
(7) ![]()
Where ![]() is the temperature of the cooling fluid.
is the temperature of the cooling fluid.
Reactivity Control Method
.Control Input Definition
The control input, reactivity ![]() , can be adjusted through various methods, such as control rod movements or chemical shim. The reactivity equation can be expressed as:
, can be adjusted through various methods, such as control rod movements or chemical shim. The reactivity equation can be expressed as:
(8) ![]()
Where:
– ![]() is the nominal reactivity.
is the nominal reactivity.
– ![]() is a gain constant.
is a gain constant.
– ![]() is the control rod position or chemical concentration change.
is the control rod position or chemical concentration change.
.Feedback Control Strategy
A feedback control strategy can be employed to maintain reactor stability. A simple proportional control can be represented as:
(9) ![]()
Where:
– ![]() is the proportional gain.
is the proportional gain.
– ![]() is the desired temperature.
is the desired temperature.
This control strategy adjusts reactivity based on the difference between the desired temperature and the current temperature, providing real-time feedback.
.Results
The simulation results demonstrate the effectiveness of the MPC strategy in maintaining stable reactor operations. Key findings include:
– Stability: The MPC successfully kept the neutron density and reactor temperature within desired limits during disturbances, such as sudden changes in coolant flow and load demands.
– Response Time: Settling times for both neutron density and core temperature were significantly reduced compared to traditional control methods.
– Control Efficiency: The control effort remained well within operational constraints, indicating the robustness of the MPC approach.
.Example Scenario
In a scenario where the reactor experiences a sudden increase in power demand, the MPC rapidly adjusts the control rods, altering the reactivity to stabilize the neutron density and temperature, thereby demonstrating the controller’s adaptability to dynamic operational conditions.
Discussion
.Advantages of MPC
The application of MPC in SMR control presents several advantages:
1. Multivariable Control: MPC effectively manages the interactions between different system variables.
2. Constraint Handling: The ability to incorporate constraints ensures that safety limits are maintained.
3. Optimal Performance: By minimizing a cost function, MPC optimally balances performance objectives and control effort.
.Challenges and Future Work
While MPC shows promise, there are challenges to address, including:
– Computational Demand: Real-time implementation may require significant computational resources, especially for complex systems.
– Modelling Accuracy: The effectiveness of MPC relies heavily on the accuracy of the underlying models.
Future work will explore enhancing model fidelity, developing adaptive MPC algorithms, and integrating advanced sensors for improved real-time monitoring and control.
Conclusion
This paper presented a comprehensive approach to controlling Small Modular Reactors using Model Predictive Control based on differential equation modelling of neutron dynamics and thermal behaviour. The developed MPC strategy effectively maintained reactor stability and optimized performance under varying conditions. As the nuclear power industry moves toward more flexible and safer solutions, the integration of advanced control strategies like MPC will be essential for the successful operation of SMRs.
