Model-free adaptive control (MFAC) is a type of control strategy that does not rely on an explicit mathematical model of the system being controlled. Instead, MFAC algorithms use feedback from the system to adjust control actions in real-time, adapting to changes in the system’s behavior.

MFAC is particularly useful in situations where the system being controlled is complex or poorly understood, and traditional model-based control approaches are difficult to apply. For example, in some industrial processes, the dynamics of the system may change over time, making it difficult to develop an accurate mathematical model that can be used for control.

MFAC algorithms typically use online learning techniques to adapt to changes in the system. The controller continuously monitors the system’s response to control actions and updates its control strategy based on this feedback. This feedback loop allows the controller to adapt to changes in the system’s behavior and achieve better performance over time.

One common approach to MFAC is reinforcement learning, which uses trial-and-error to learn an optimal control policy for the system. In reinforcement learning, the controller takes actions in the system and receives feedback in the form of a reward signal, which is used to update the control policy. Over time, the controller learns to take actions that maximize the expected reward, leading to improved performance.

Another approach to MFAC is adaptive control, which uses mathematical techniques to adjust the controller’s parameters in response to changes in the system. Adaptive control can be particularly useful in situations where the system’s dynamics are well understood, but may change over time due to external factors.

Overall, MFAC is a powerful approach to control that can be applied in a wide range of settings. By adapting to changes in the system’s behavior in real-time, MFAC can help to achieve better performance and improve the overall efficiency and reliability of the control process.

A MFAC control system is defined to have the following properties:

No precise quantitative knowledge of the process is available.
No process identification mechanism or identifier is included in the system.
No controller design for a specific process is needed.
No manual tuning of controller parameters is required.
Closed-loop system stability analysis and criteria are available to guarantee the system stability.

Derivations of the core MFAC control technology address specific control problems as described here:

SISO MFAC to replace PID so that manual controller tuning is eliminated
Nonlinear MFAC to control nonlinear processes
MFA pH controller to control pH processes
Feedforward MFA controller to deal with measurable disturbances
Anti-delay MFAC to control processes with large time delays
Robust MFAC to protect the process variable from running outside a bound
Time-varying MFA controller to control time varying processes
Anti-delay MFAC pH controller for pH processes with varying time delays
MIMO MFAC to control multivariable processes

MFAC controllers can be readily embedded into various control equipment and are becoming available on more and more platforms offered by multi-vendors including building controllers, single-loop controllers, programmable logic controllers (PLC), hybrid controllers, process automation controllers (PAC), control software, and distributed control systems (DCS).

Single-Loop MFA Control System

Figure 1.1a depicts a single-loop control system using Model-Free Adaptive (MFA) control, comprising a single-input single-output (SISO) process, a SISO MFA controller, and a feedback loop. The goal of the controller is to generate an output $u(t)$ that drives the process variable $y(t)$ to track the desired setpoint trajectory $r(t)$ , while handling variations in setpoint, disturbance, and process dynamics. To achieve this, the MFA controller minimizes the error $e(t)$ between the setpoint and the process variable in real-time, by regulating the control and adjusting its weighting factors to adapt to dynamic changes, disturbances, and other uncertainties of the system.

Figure 1.1a [Single-loop MFA control system.]

Figure 1.1b shows the structure of a single-input single-output MFA controller, which employs a multilayer perceptron (MLP) artificial neural network (ANN) for its design. The ANN has an input layer, a hidden layer with N neurons, and an output layer with one neuron. The neural network contains a set of weighting factors ( $w_{ij}$ and $h_{i}$ ) that can be updated to alter the behaviour of the dynamic block. The update algorithm aims to minimize the error between the setpoint and process variable, which aligns with the control objective, and enables the controller to minimize the error despite changing process dynamics.

Alternatively, the MFA controller based on the ANN remembers a portion of the process data, which provides valuable insights into the system’s dynamics. In contrast, the digital version of the PID controller only stores the current and two previous samples, which implies that PID has minimal memory. In comparison, MFA possesses the memory necessary for an intelligent controller.

Figure 1.1b [Architecture of a SISO MFA controller].

SISO MFA Controller Algorithm

The core MFA control algorithm comprises the following difference equations:

(1) $\begin{equation*} p_{j}(n) = \sum_{i=1}^{N} w_{ij} (n) E_{i}(n) + 1 \end{equation*}$

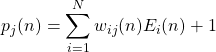
(2) $\begin{equation*} q_{j}(n) = \varphi (p_{j}(n)) \end{equation*}$

(3) $\begin{equation*} o(n) = \Psi [ \varphi (\sum_{j=1}^{N} h_{j} (n) q_{j} (n) + 1)] = \sum_{j=1}^{N} h_{j} (n) q_{j} (n) + 1 \end{equation*}$

(4) $\begin{equation*} v(t) = K_{c}[o(t) + e(t)] \end{equation*}$

where n denotes the nth iteration, $o(t)$ is the continuous function of $o(n)$ , $v(t)$ is the output of the MFA controller, $K_{c} > 0$ and is the MFA controller gain, and $w_{ij}$ and $h_{j}$ are weighting factors.

The weighting factors can be updated online at every sample interval using the following formulas:

(5) $\begin{equation*} \triangle w_{ij} (n) = \eta K_{c}e(n)q_{j}(n)(1-q_{j}(n))E_{i}(n) \sum_{k=1}^{N} h_{k}(n) \end{equation*}$

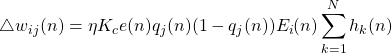
(6) $\begin{equation*} \triangle h_{j} (n) = \eta K_{c}e(n)q_{j}(n) \end{equation*}$

MFA and PID

Although most industrial processes are currently controlled using PID (proportional–integral-derivative) controllers, these controllers have limitations when it comes to controlling complex systems. In addition, PID controllers require frequent manual tuning of their parameters when the process dynamics change.

For example, when starting from the same oscillating control condition, a system controlled by PID will continue to oscillate, while a system controlled by MFA will quickly adapt to an excellent control condition. Furthermore, when both controllers start from a sluggish situation, MFA can control the process faster and more effectively.

MFA Control System Requirements

As a feedback control system, MFA requires the process to have the following behaviour:

The process is controllable.
The process is open-loop stable.
The process is either direct or reverse acting (process does not change its sign).

If the process is not controllable, improvement of the process structure or its variable pairing is required. If the process is not open-loop stable, it is always a good practice to stabilize it first.

However, for certain simple open-loop unstable processes such as a non-self-regulating level loop, no special treatment is required when using MFA. If a process changes its sign within its operating range, special MFA controllers are required.

SISO MFA Configuration

A SISO MFA controller requires only a few parameters to be configured, including the sample interval, controller gain, time constant, and acting type of the process. The sample interval determines the frequency at which calculations are made, with high-speed MFA controllers capable of running at rates as fast as 1 millisecond. While a default controller gain value is recommended, the time constant provides a rough estimate of the process time constant in seconds. The acting type of the process can be either direct or reverse, depending on whether an increase in the process input leads to an increase or decrease in the output, respectively. It is important to note that MFA controllers embedded in different platforms may use varying definitions for controller acting type.

According to information theory principles, the sample interval should be less than or equal to one-third of the time constant, as expressed by the inequality $T_s \le (1/3)T_c$ , where Ts represents the sample interval and Tc represents the time constant. Once the configuration is complete, MFA can be launched at any time and will immediately control the process without requiring process identification or dynamic modeling. Additionally, MFA controllers can be switched between automatic and manual modes at any time without requiring a specific bump-less transfer procedure.

Nonlinear MFA Controller

Controlling nonlinear systems can be a difficult task, as the nonlinear behavior of the process can vary greatly, making it challenging to develop a single controller to handle all nonlinear processes. Traditionally, the approach has been to linearize the nonlinear process by adding a reverse nonlinear function to compensate for the nonlinear behavior. However, this can be a tedious process, and uncertainties in the process can cause problems.

The nonlinear MFA controller offers a more uniform solution to nonlinear control problems. It is suitable for controlling processes with nonlinear sensors, actuators, and other elements. One example of a nonlinear process is a flow or high-pressure loop, where different operating conditions can cause the actuator to lose its authority. In addition, wear and tear on a valve can make it nonlinear.

Another example of a nonlinear process is the dissolved oxygen in a bio-tech micro reactor used for cell cultivation. As the number of cells grows, they start to consume more oxygen, which can cause difficulties in controlling the process. With the general-purpose nonlinear MFA controller, the challenges of controlling nonlinear processes such as this can be overcome more easily and cost-effectively.

Nonlinear MFA Configuration

The nonlinear MFA controller requires an additional parameter, known as the process nonlinearity factor, in addition to the parameters used in SISO MFA such as sample interval, time constant, controller gain, and acting type.

The process nonlinearity factor is a number between $0$ and $10$ , with $10$ representing an extremely nonlinear process and $0$ representing a linear process. The nonlinear MFA controller does not rely on the specific nonlinear characteristics of the process. For example, a valve can be either “fast open” or “fast close,” as represented by convex and concave curves.

With the nonlinear MFA controller, there is no need to determine the layout of the nonlinear curve. The curve can be concave, convex, or S-shaped, and the controller only requires information on the degree of nonlinearity: whether the process is extremely nonlinear (enter a $9$ or $10$ ), quite nonlinear (enter a $5$ or $6$ ), or somewhat nonlinear (enter a $1$ or $2$ ). The nonlinear MFA controller can handle the rest.

Simulations and real applications demonstrate that the nonlinear MFA controller can effectively manage nonlinear processes even if the gain changes frequently. The MFA controller gain $K_c$ is set at its nominal point and does not require retuning, and there is no need for linearization calculations or process models in the nonlinear MFA controller.

MFA pH Controller

pH control is a crucial aspect of most process plants, as the wastewater effluent generated must be neutralized before discharge or reuse. However, a significant percentage of pH loops do not perform well, resulting in inferior product quality, environmental pollution, and material waste. With increasing pressure to improve plant efficiency and tighter regulations in environmental protection, effective continuous pH control is essential.

A highly nonlinear pH process is observed in a strong-acid-strong-base system. The pH value has a logarithmic relationship with the reagent flow, and the process gain is relatively small away from neutrality. However, near neutrality where pH = 7, the process gain can be a few thousand times higher. Fixed controllers like PID are not effective in controlling this process, and most pH loops are typically in a “bang-bang” type of control, leading to large oscillations when pumps turn on and off.

Over-dosing acid and caustic is not desirable as it incurs additional costs. Statistics indicate that poorly controlled pH processes can cost thousands of dollars in chemical usage each month, not to mention the penalties imposed by violating discharge codes.

The adaptive capability of the MFA pH controller enables it to compensate for the large nonlinear gain changes, making it able to control a wide range of pH loops. In addition, it allows for high-precision control of the full pH range and enables automatic control of acid or alkaline concentration, both critical quality variables for the chemical process industry.

Feedforward MFA Controller

Feedforward control is a strategy utilized to mitigate disturbance signals in a control system. By anticipating the effects of a measurable disturbance, a feedforward controller can improve control system performance and reduce the need for corrective action from the feedback loop. This method can be as simple as a ratio between two signals or may involve complex calculations based on energy or material balance. The feedforward MFA is a versatile feedforward controller that does not attempt perfect disturbance cancellation, which can be challenging to achieve in industrial applications due to changing process dynamics and operating conditions.

A feedback/feedforward MFA control system diagram is illustrated in Figure 1.1f, where $G_{p}1$ is the main process and $G_{p}2$ is the process with disturbance input and the process variable as output.

Figure 1.1d [Feedback and feedforward MFA control system.]

A feedback/feedforward MFA control system diagram is depicted in Figure 1.1f, where $G_{p}1$ represents the primary process, and $G_{p}2$ is the process with the disturbance input and the process variable as the output. Since the feedback MFA controller possesses strong adaptive capabilities, the feedforward MFA can be designed in a straightforward manner, with two parameters to configure: the feedforward controller gain and time constant. The feedforward controller gain can be estimated using the static gains of processes $G_{p}1$ and $G_{p}2$ , which determines the extent to which the feedforward action rejects the disturbance. The sign of the feedforward gain can be selected based on whether processes $G_{p}1$ and $G_{p}2$ have the same or different signs. The feedforward MFA time constant can be estimated using the time constant of $G_{p}2$ , which indicates how quickly the disturbance will impact the process variable.

Anti-delay MFA Controller

Many industrial processes experience significant time delays due to the time it takes for heat, materials, and signals to be transformed. This delay can make it impossible to measure the effect of control actions in real-time, effectively disabling the feedback loop that is essential for automatic control.

Using a PID controller to control a process with large time delays can result in significant overshoot or instability, requiring the controller to be detuned, sacrificing control performance. Generally, a PID controller can only work effectively when the τ-T ratio (delay time over time constant) is less than one.

The Smith predictor is a useful control scheme for processes with large time delays, but constructing a precise process model is usually necessary for optimal performance.

An alternative approach is the SISO anti-delay MFA control system, as shown in Figure 1.1g. This system uses an anti-delay MFA controller and a delay predictor to produce an artificial dynamic signal that replaces the delayed process variable as the feedback signal.

The MFA controller in this system has adaptive capabilities, enabling the delay predictor to be designed in a simple form without precise quantitative information about the process. An estimated delay time is sufficient, and the controller can handle delay times that are two to five times larger or smaller than the actual delay time.

This approach is particularly useful for controlling process quality variables, as it can achieve six sigma or zero defects quality control objectives. In semicontinuous production environments, where line speed changes frequently, the delay time can be easily calculated and provided to the anti-delay MFA controller in real-time.

However, if the delay time of a process changes on a scale of more than five times, and the delay time information cannot be provided to the controller, a time-varying MFA controller may be more appropriate.

Robust MFA Controller

Complex control applications pose several challenges, such as the need for prompt control action when a large change in system dynamics occurs, difficulty in implementing feedforward compensation due to an economically unmeasurable dominant disturbance, the risk of losing control when a controller is detuned to minimize variations in the manipulated variable, and the lack of triggering information to switch operating modes.

For example, controlling the temperature in a batch reactor is a challenging task due to various factors such as potential disturbances, variable interactions, and multiple operating conditions. Many batch reactors cannot maintain automatic control over the entire operating period, leading to lower efficiency, inconsistent product quality, and wastage of resources.

During the transition period from the reaction and holding stage to the no-reaction and holding stage in an exothermal batch reactor, the control system must react quickly to cut off cooling water and introduce steam to maintain the reactor temperature. However, a regular feedback controller is inadequate during this transition period, and the batch reactor usually requires manual control by well-trained operators, which can result in low product quality and yield.

The robust MFA controller can effectively handle these challenges without requiring controller redesign, feedforward compensation, or retuning of controller parameters. This controller can maintain automatic control over the system during normal and extreme operating conditions, including significant disturbances or dynamic changes.

Robust MFA Controller Configuration

Configuring the robust MFA controller involves setting the following parameters:

Upper and lower bounds: These bounds define the allowable range for the process variable (PV) being controlled. They serve as intelligent boundaries that the PV should not exceed. Unlike the controller output (OP), which can have hard limits or constraints, the PV can only be controlled by manipulating the OP. Therefore, the upper and lower bounds for PV are distinct from the OP constraints.

Gain ratio: This coefficient determines how much the MFA control action should be increased or decreased. A gain ratio of 3 is recommended, indicating that the MFA gain in abnormal situations is three times higher than the regular MFA gain setting. It is important to note that this is not a gain scheduling approach, despite appearances. Gain scheduling is unable to resolve the complex problems described.

Time-Varying MFA Controller

The time-varying MFA controller is a suitable option for controlling a process that exhibits large variations in time constant and/or delay. For example, in a temperature control loop, the time constant may vary significantly depending on whether the process is heating up or cooling down, as adding heat to the process is much quicker than removing it. Similarly, variations in line speed or flow rate can result in significant changes in process delay time.

To configure the time-varying MFA controller, it is necessary to estimate the minimum and maximum process time constant plus delay time. Once configured, the controller can handle the changes in time constant and/or delay time, without requiring any parameter retuning.

Anti-delay MFA pH Controller

By combining the time-varying MFA and MFA pH control functions, an anti-delay MFA pH controller can be created, which can effectively control a pH process with large and varying time delays. In situations where the pH process has large inflow rates, pH changes, and varying time delays, the control loop becomes extremely challenging. The large gain changes with varying time delays exacerbate the situation, making the process almost “uncontrollable.” Traditionally, “bang-bang” type control or batch-based pH neutralization was the only viable option. However, the anti-delay MFA pH controller is both predictive and adaptive, making it robust enough to handle inflow changes, titration curve movements, and other uncertainties. It can predict and adapt to large gain changes, deal with large time delays, and maintain stability under challenging conditions.

Multivariable MFA Control System

Figure 1.1e illustrates a multivariable feedback control system with a model-free adaptive controller. The system includes a multi-input multi-output (MIMO) process, a set of controllers, and a set of signal adders, respectively, for each control loop.

Similar to a SISO system, the MIMO system has controller setpoints $r(t)$ , error signals $e(t)$ , controller outputs $u(t)$ , process variables $y(t)$ , and disturbance signals $d(t)$ . Since it is a multivariable system, all the signals here are vectors represented in bold type.

Figure 1.1e [Multivariable MFA control system.]

Two-input Two-output MFA Control System

Without losing generality, we will show how a multivariable model-free adaptive control system works with a two-input two-output (2 × 2) system as illustrated in Figure 1.1k, which is the 2 × 2 arrangement of Figure 1.1e. In the 2 × 2 MFA control system, the MFA controller set consists of two controllers – $C_{11}$ and $C_{22}$ – and two compensators – $C_{11}$ and $C_{22}$ . The process has four subprocesses – $G_{11}$ , $G_{21}$ , $G_{12}$ , and $G_{22}$ .

The measured process variables $y_{1}$ and $y_{2}$ are used as the feedback signals of the main control loops. They are compared with the setpoints $r_{1}$ and $r_{2}$ to produce errors $e_{1}$ and $e_{2}$ . The output of each controller associated with one of the inputs, $e_{1}$ or $e_{2}$ , is combined with the output of the compensator associated with the other input to produce control signals $u_{1}$ and $u_{2}$ .

Figure 1.1f [Two-input two-output MFA control system.]

The output of each subprocess is cross-added to produce measured process variables $y_{1}$ and $y_{2}$ . Notice that in real applications the outputs from the subprocesses are not measurable and only their combined signals $y_{1}$ and $y_{2}$ can be measured.

Thus, by the nature of the 2 × 2 process, the inputs $u_{1}$ and $u_{2}$ to the process are interconnected with outputs $y_{1}$ and $y_{2}$ . The change in one input will cause both outputs to change.

The control objective for this 2 × 2 MFA control system is to produce control outputs $u_{1}(t)$ and $u_{2}(t)$ to force the process variables $y_{1}(t)$ and $y_{2}(t)$ to track their setpoints $r_{1}(t)$ and $r_{2}(t)$ , respectively.

The minimization of $e_{1}(t)$ and $e_{2}(t)$ is achieved by:

The regulatory control capability of the MFA controllers
The decoupling capability of the MFA compensators
The adjustment of the MFA weighting factors, which allow the controllers to deal with the dynamic changes, large disturbances, and other uncertainties

2 x 2 MFA Controller Configuration

A 2 × 2 MFA controller can be considered to have two main controllers, $C_{11}$ and $C_{22}$ . For each main controller, the parameters to configure are:

Sample interval – the interval between two samples or calculations in seconds. A high-speed MFA controller can run at a 1 millisecond rate.
Controller gain – use of a default value is recommended.
Time constant – a rough estimate of the process time constant in seconds.
Acting type – direct or reverse acting of the process.
Compensator gain – to deal with the interaction from the other loop.

MIMO MFA Controller Application Guide

A MIMO system can be much more complex than a SISO system; precautious have to be taken when applying a MIMO MFA controller. When designing a multivariable control system, the first step is to decide which process variable is paired with a manipulated variable. A MIMO MFA control system should follow these pairing rules:

Each process of the main loops has to be controllable, open-loop stable, and either reverse or direct acting.
A process with a large static gain should be included in the main loop as the main process ( $G_{11}$ , $G_{22}$ ), and a process with a small static gain should be treated as a subprocess ( $G_{21}$ , $G_{12}$ ).
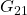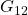A faster process should be paired as the main process and a slower process, and processes with time delays should be treated as subprocesses.
If pairing rules 2 and 3 should result in a conflict, a tradeoff is the only option.

In addition, an MFA control system should be designed based on the degree of interactions between the loops. Table 1.1j lists the control system design strategy based on the degree of interaction of a MIMO process.

Table 1.1j [MIMO System Design Strategy.]

MFA Control Methodology

MFA (Model-Free Adaptive) control methodology is a type of control system that uses an adaptive algorithm to adjust control actions based on real-time process measurements without the need for a mathematical model of the process. The MFA control methodology is designed to handle complex processes with non-linear behavior, large variations, and disturbances.

The MFA control methodology uses a control algorithm that includes an online estimator and a controller. The online estimator uses real-time process measurements to estimate the process gain and time constant, and then feeds these estimates to the controller. The controller then calculates the control action based on the estimated process parameters and the desired setpoint.

The MFA control methodology can be used for a wide range of control applications, including temperature control, pH control, pressure control, and flow control. It is particularly useful for controlling complex chemical processes with significant variations and disturbances.

The MFA control methodology has several advantages over traditional control methods. First, it does not require a mathematical model of the process, which can be difficult or impossible to obtain for complex processes. Second, it is adaptive and can adjust to changes in process behavior and disturbances in real-time. Third, it is robust and can handle uncertainties and variations in the process.

Overall, the MFA control methodology is a powerful tool for controlling complex processes and can provide significant benefits in terms of efficiency, quality, and productivity.

Summary

To develop the MFA control method based on the combined intelligence methodology, four key points are considered.

Firstly, a dream controller needs to be simple yet powerful enough to control various complex processes. While PID control is easy to understand, it may not be effective for more difficult control problems. Model-based advanced control methods, on the other hand, are too complex to launch and maintain. MFA provides a solution that is powerful enough to control complex processes yet simple enough to use, launch, and maintain.

Secondly, MFA uses all available process information, such as the process time constant, acting type, static gain, and delay time, to design a controller. This makes MFA an information-based controller.

Thirdly, MFA’s adaptive capability can handle changes, uncertainties, and disturbances that arise in a gray box process, which is a process with an unclear input-output relationship.

Lastly, MFA is neither model-based nor rule-based but is an information-based control method that focuses on delivering a simple, adaptive, and effective solution. A series of MFA controllers has been developed to address different difficult control problems, and users can select the appropriate MFA, configure its parameters, launch the controller, and reap the benefits.

CT.04 / Model-Free Adaptive Control +