Digital Control Algorithms

The Ziegler and Nichols tuning rules were developed based on the limitations of the analog controllers that were commonly used in the past and still are used today. However, with the introduction of digital controllers, designers and programmers have been able to create more sophisticated algorithms that are not limited by mechanical or electronic constraints. As a result, many digital controller manufacturers offer multiple algorithms, and in laboratory settings, non-vendor computers may be used with custom-written control algorithms that combine classical and non-classical approaches. When working with non-classical algorithms, caution should be exercised when applying classical tuning rules, as the programmer may not have a thorough understanding of control loop dynamics upon which the tuning rules are based.

Different terms are used to describe the variations from the traditional algorithm. Some refer to the traditional as “interacting,” while others refer to variations as “non-interacting.” Another term used for the traditional algorithm is “series,” while variations are sometimes called “parallel.” When the controller uses only P or I, the algorithm is usually not important, unless it was developed in-house. However, when the controller uses PID, it is best to use the traditional algorithm to ensure that the tuning rules apply. Although there may be certain cases where the newer algorithm is preferred. If the controller is PI (or PID, which is not commonly used) or if it is a PLC, there are so many possibilities that a general rule cannot be given.

Figure 9.1 [The difference between a series and a parallel algorithm is shown conceptually in this signal-flow diagram.]

Math / Algebra

The conceptual differences between the two basic forms for the algorithm are shown in the equations below. For the older or series or interacting algorithm the transfer function has the following general form:

(1) $\begin{equation*}P(1+I)(1+D)\end{equation*}$

The Laplace transform for this is:

(2) $\begin{equation*}K_{C}\left(1+\frac{1}{T_{i}s}\right)\left(\frac{T_{d}+1}{\frac{T_{d}}{K_{d}}s+1}\right)\end{equation*}$

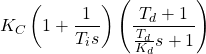
For the algorithms that became available with digital computers, which have been called parallel or non-interacting, the transfer function has this general form:

(3) $\begin{equation*}P+I+D\end{equation*}$

The Laplace transform for this becomes:

(4) $\begin{equation*}K_{C}+\frac{1}{T_{i}s}+\frac{T_{d}s}{\frac{T_{d}}{K_{d}}s+1}\end{equation*}$

Theoretically, it is possible to match two transfer functions by equating similar terms. However, we typically rely on the well-known algorithm unless we are dealing with custom software. In such cases, some algebraic manipulation may be required to convert the function to the familiar form. If we are working with custom software, we may try to convince the programmer to use the series algorithm.

Sampling Frequency and Loop Performance

Digital controllers sample measurements periodically at a frequency known as the sampling frequency or cycle time, unlike analogue controllers that measure continuously. This periodic measurement has two potential downsides. Firstly, it may introduce an unwanted lag, causing digital control to be slower than analogue control. Secondly, it can lead to the loss of useful information.

The incremental effective dead time caused by the lag is between half the cycle time and 1.5 times the cycle time. As discussed previously, a sampling period of 0.25 seconds (4 times per second) is usually sufficient for most loops, unless derivative action is required. Commercial controllers typically sample 10 times per second, which is sufficient for most process industry loops, but may not provide adequate derivative response for faster loops.

Consider a device with a cycle time of one second. If it instantly measured and produced an output based on that measurement, the effective dead time would be 0.5 seconds. However, if it measured, then calculated, and produced an output one second later (just before the next measurement), the effective dead time would be 1.5 seconds. Thus, the incremental effective dead time added is half the cycle time plus the full time between the measurement and the output based on that measurement.

Figure 9.2 [If a cycle is not sampled often enough it will look like a longer cycle, and create havoc..]

When using digital controllers, there are several potential issues to consider due to the periodic nature of the sampling process, which is performed at a frequency known as the sampling frequency or cycle time. The first issue is the potentially undesirable lag that can be introduced, making digital control slower than analogue control. Additionally, information may be lost due to the periodic nature of sampling. To address the lag, an effective dead time of half the cycle time to 1.5 times the cycle time is introduced.

Another concern arises if the cycle time is long relative to the potential variations in the process. If the sampling system samples fewer than twice per period of the process variations, a numerical problem called aliasing can occur, where the variability that is happening too fast for the sampling system to reconstruct is pushed over into longer periods. This is especially relevant when providing digital derivative action, as the sampling rate needs to be significantly higher than the derivative time setting. In general, using derivative action in a digital controller for relatively fast processes is not recommended.

It is difficult to determine an appropriate sampling frequency to avoid aliasing, but it is important to be aware that sampling introduces problems beyond simple lags. While a digital controller can approach the dynamic performance of an analogue controller, it is unlikely to reach the same level of performance. If the sampling rate is slowed down to allow one CPU to handle many loops, performance may be reduced, but this becomes an economic decision. In general, most sampling rates are likely based on what is available, and the resulting performance is a by-product.

Load Changes / Upsets / Disturbances

The disturbances in a control loop can be known or unknown, and their effects can also be known or unknown, which adds a level of complexity to control systems. This can make control systems more of an art than an exact science. When examining recording charts to diagnose performance, it can sometimes be easy, but at other times it can be next to impossible.

For example, a flow control loop is usually fast and the reasons for flow changes are well understood. Therefore, any effects that last too long can be judged as unnecessary and fixable through tuning or hardware improvements. In contrast, composition control systems are usually slow, and the source of disturbances may be a mystery, making it difficult to determine whether the loop is performing as well as it can without retuning.

In between these two extremes, experience and knowledge are essential in diagnosing performance. If a control system has been giving excellent performance and then performs poorly, it may be helpful to look for a coincident cause. It can be challenging to make general comments about a system that was drawing straight lines and now appears to be drawing less straight lines, so it is important to use all knowledge gained about what affects the performance of a loop.

One practical step to consider is putting the loop on manual to see if the situation improves or worsens, especially in situations where interaction is suspected.

Dampening Noisy Measurements

At times, a noisy measurement may prevent the controller from being set to the desired gain. This can result in excessive valve movement, leading to further deterioration of the situation, along with increased valve wear and instrument air consumption. While solving this issue may be straightforward in some cases, it can be challenging in others. In this section, we will explore the use of a first order lag and the Moore Products inverse derivative unit as means of addressing this problem. While computer-based options may offer more elegant solutions, we will not delve into those here.

The first order lag is a widely used filter because of its relative ease of implementation and broad understanding. Many instruments, such as transmitters, come equipped with adjustable damping, which is usually implemented as a first order lag. In digital equipment, a first order lag can be approximated with minimal storage and operations. While its behavior has been explained in terms of its time response (as seen in figure 4.5), understanding its response to cyclic upsets in frequency or period terms can be more helpful.

In the time domain, the observed reading changes at a rate such that it would reach the true value in one time constant. While this information is crucial, it can be challenging to apply. The key to filtering or damping noisy measurements is to minimize the undesired signal while retaining the desired signal. The first order lag is known as a “low pass” filter, meaning it attenuates high frequencies while allowing low frequency variations to pass through. Therefore, when using a first order lag to dampen noisy measurements, it is assumed that the desired signal can be distinguished from the undesired signal based on frequency or period.

However, the separation between what is attenuated and what is not is not a sharp one. For example, the filter will not allow one cycle per minute to pass through while significantly attenuating 1.1 cycles per minute. Moreover, noise is usually not made up of a single frequency but rather consists of multiple components. A helpful way to think about this is to imagine filtering sections of the noise signal with sections of sine waves of different frequencies, which can aid in making the necessary decisions.

A simplified formula for the attenuation characteristic of a first order lag is:

(5) $\begin{equation*}\frac{Output\ amplitude}{Input\ amplitude}=\frac{P}{6.28T}\end{equation*}$

Where:

$P$ = Period, same time units as $T$

$T$ = Time constant of filter

It should be noted that the ratio in the formula cannot exceed one. Therefore, the formula is only valid when $P$ is less than $6.28T$ . However, if the goal is simply to achieve some degree of attenuation, this is sufficient information. The complete equation for the amplitude ratio can be found in chapter 4, in the math/algebra section for the first order lag. Although using a first order lag to reduce noise can be effective, it can also introduce a lag that affects the apparent dead time and, as a result, degrade loop performance.

When the periodicity of the noise is close to the natural period, reducing the gain and integral time together can be a good compromise. For example, if the standard tuning rules suggest a gain of 5 and an integral time of 10 minutes, consider using a gain of 3 and an integral time of 6 minutes, or a gain of 1 and an integral time of 2 minutes. However, for non-self-regulating loops like level control, an integral-only controller is not recommended as it can lead to cycling problems.

If your loop is pneumatic, the Moore Products pneumatic relay, Model 59R, may be worth considering. This reverse action derivative relay can reduce high frequency amplitudes by a factor of 6 and has a time adjustment to specify which frequencies are not attenuated. It can be implemented easily and is typically placed in the output of the controller, although it can be placed on the input in certain circumstances. Its advantages are difficult to explain without frequency response analysis, but it may be helpful in minimizing the effect of the filter on the natural period in certain situations. Additionally, it is worth noting that dampening a recording is acceptable to improve readability, but it is important to remember that the true nature of the signal may be worse than what is observed.

Math / Algebra

The amplitude ratio for a first order lag, which is what a simple filter is, was given as:

(6) $\begin{equation*}\frac{1}{\sqrt{1+(\omega T)^{2}}}=\frac{1}{\sqrt{1+\left(\frac{6.28T}{P}\right)^{2}}}\end{equation*}$

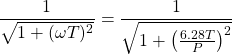
This quantity is always less than one. For the lag to give significant attenuation the $\omega$ T term must be significantly larger than one, in which case the above terms approximate these:

(7) $\begin{equation*} \mathrm{Amplitude\ ratio} =\frac{1}{\omega T}=\frac{P}{6.28T}\end{equation*}$

The attenuation is the reciprocal of the amplitude ratio.

PID.09 / PID Control Structure +

Digital Control Algorithms

Math / Algebra

Sampling Frequency and Loop Performance

Load Changes / Upsets / Disturbances

Dampening Noisy Measurements

Math / Algebra