Enterprise-wide optimization is the ultimate level of optimization that involves optimizing not just the manufacturing process but also the supply chain of raw materials and the distribution chain of products and packaging. It is a more significant level of optimization than process optimization as it demands the concurrent evaluation of all three areas of optimization. The objective is to devise operational strategies that keep all three areas operating at their optimal levels (as shown in Figure 1.1a).

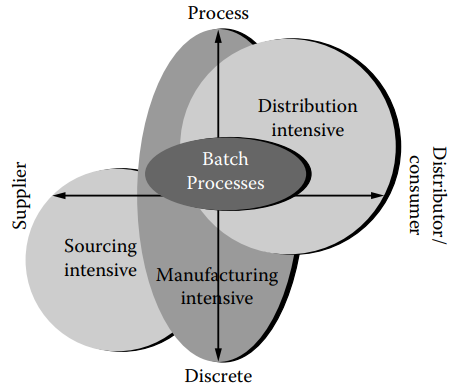
Figure 1.1a [Enterprise-wide optimisation requires the optimisation of not only the manufacturing plant but also the raw material supply chain and the product distribution chain].

Plant-wide optimization involves more than just optimizing individual unit processes. It also takes into account documentation, maintenance, scheduling, and quality management considerations. This involves finding solutions to potentially conflicting objectives of the various unit operations and developing strategies to optimize the entire plant.

At the unit operations level, it is essential that each processing equipment is functioning properly and that control loops are properly tuned for multivariable optimization. Sampling measurements at a fast enough rate and tuning loops for fast recovery rates are also important factors. Interactions between loops must be eliminated or corrected to avoid loop cycling. In cases where there is no mathematical model to describe a process and empirical optimization is required, experimental optimization becomes necessary. This section delves into this topic.

Empirical Optimisation

Theoretical mathematical models can be used to describe the performance of certain processes, and mathematical techniques can be applied to determine the optimal operating conditions that meet specific performance criteria. However, many processes do not have sufficient mathematical models, and these processes are known as empirical processes. To optimize empirical processes, experimentation is required. This section focuses on methods for finding optimal process settings through experimentation, with a particular emphasis on the Ultramax method. This method is suitable for a wide range of processes and is supported by user-friendly computer tools.

Optimisation

In this context, the term “optimize” is used to refer to achieving a specific measurable criterion or quality ( $Q$ ) of the process. This can involve maximizing or minimizing $Q$ depending on the user’s objectives. For instance:

Maximizing plant production rate
Minimizing cost-per-ton of output
Maximizing flavor of a product
Maximizing the height/width ratio of a chromatograph peak

$Q$ is also known as the objective function or target variable. Sometimes, several criteria may need to be weighted to produce a single measurement of process performance. However, for the sake of simplicity, the examples discussed here will focus on maximizing the value of $Q$ .

Optimizing the process may also involve ensuring that other measured results of the process ( $R$ , $S$ , etc.) remain within specified limits. For instance, maximizing plant production rate for butter, paper, or sulfuric acid must be subject to a specified limit on water content in each product.

Information Cycle Times

Certain processes require a long period of time to collect information and evaluate the performance of different variations. For instance, determining the optimal resistance to weathering of paint formulations or finding the most productive mixture of synthetic fertilizers for farmland may take an unacceptably long time if one test is performed at a time. To overcome this limitation, multiple formulations of paints or fertilizers are planned and simultaneously tested. This strategy is referred to as parallel design of experiments and involves planning, executing, and analyzing multiple experiments at once.

Parallel Design

Consider the example of a process that involves baking a material for a duration of time ( $D$ ) at a specific oven temperature ( $T$ ) to achieve a desirable quality ( $Q$ ) which needs to be maximized. This process could be the case-hardening of steel, polymerization of resin, or ion diffusion in silicon chips. Only $D$ and $T$ can be adjusted to affect $Q$ , while other variables remain constant. The process is conducted at various combinations of $D$ and $T$ , and the corresponding $Q$ values are recorded.

The optimal values for $D$ and $T$ can be determined by drawing contours of $Q$ on a graph representing the different $D$ and $T$ values. The highest point on the hill corresponds to the optimal conditions for the process. The contours of $Q$ are also known as the response surface of the process and can be mathematically fitted to the data points rather than drawn by hand. This approach is particularly helpful when the process involves several manipulated variables. The statistical texts refer to $D$ and $T$ as the controlled variables, while engineers call them manipulated variables, and $Q$ is referred to as the controlled variable. Several computer programs are available for parallel designs of experiments, which are useful for experienced industrial statisticians.

Sequential Design

In some cases, processes have short information cycle times, and the results from using specific process settings are available in time to determine the settings for the next test. This approach is known as sequential design of experiments or hill climbing.

Using the previous example, the hill-climbing process involves evaluating three different values for the settings $D$ and $T$ . The slope of the response surface, defined by the values of $Q1$ , $Q2$ , and $Q3$ , indicates the direction to increase $Q$ . The next values for $D$ and $T$ are selected to proceed in this direction, and the experimenter continues to hill-climb step by step towards the maximum value for $Q$ .

However, if the process has many independent variables and noise that affects the results, it can be challenging to determine how each variable is impacting the product quality ( $Q$ ). The Simplex search procedure can find the maximum value of $Q$ with one more process result than the number of independent variables. In this case, it would require three process results.

Figure 1.1b illustrates the Simplex search method. To find the next settings for the process, a line is drawn from the settings with the lowest result, through the midpoint of the opposite face, to an equal distance beyond. In this example, the search reaches the optimum with 20 data points.

The Simplex search was developed by William Spendley at ICI Billingham, England, to automate the evolutionary operation (EVOP) procedures of G. P. Box and others. These methods can be implemented using paper and pencil or a desk calculator.

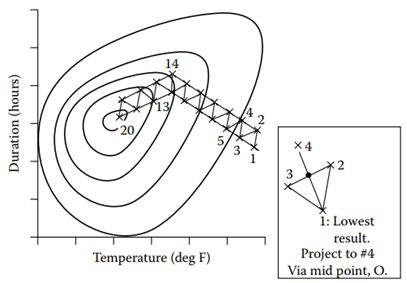
Figure 1.1b [SIMPLEX search for a maximum of quality, $Q$ . Contours of $Q$ are shown, though usually unknown. Inset shows how the next process settings are found. Direction changes where #14 has lower $Q$ than #13].

Bayesian Method

Bayesian optimization is a technique typically used to solve problems of the form $max_{x \in A} f(x)$ , where $A$ is a set of points that can be easily evaluated for membership. This method is especially useful when $f(x)$ is difficult to evaluate, has unknown structure, relies on fewer than 20 dimensions, and lacks derivatives.

The Bayesian approach considers the objective function as a random function and assigns a prior distribution to it that captures beliefs about its behavior. After gathering function evaluations, which are treated as data, the prior is updated to form the posterior distribution over the objective function.

The posterior distribution is then used to construct an acquisition function, also known as infill sampling criteria, that determines the next query point. There are several methods to define the prior/posterior distribution, with the most common being Gaussian Processes using a technique called Kriging. Another method is the Parzen-Tree Estimator, which constructs two distributions for ‘high’ and ‘low’ points, and then finds the location that maximizes the expected improvement.

Exotic Bayesian optimization problems arise when the evaluations are not easy, parallel, or involve trade-offs between difficulty and accuracy. Environmental conditions and derivatives can also complicate the evaluation. These problems require modifications to the standard Bayesian optimization technique.

Conclusion

The development of methods for optimizing empirical processes has been heavily influenced by the work of James M. Brown, who made significant contributions in this field. These methods were initially used exclusively by statisticians with specialized knowledge, but today they have been adapted for use by engineers.

While many companies that use these optimization techniques do not publicize their successes, resources and support for implementing these methods are readily available from providers of optimization software. As a result, engineers are now able to utilize these tools to achieve optimal results in their respective industries.