The term “lag” is a broad concept that refers to any situation in which a particular result occurs after a cause. On the other hand, the term “lead” can be considered the opposite of lag, although it should be noted that a result cannot occur before a cause. The concept of lags is essential for understanding control, and there are different levels of understanding, but it is possible to gain a useful amount of training without delving too deeply. While no formal proofs will be presented, the reasoning behind the concepts discussed should be consistent with one’s cognitive abilities.

In practice, the precise mathematical characterization of lags can be extremely intricate and may even defy definition. However, this is of little consequence since their impact on a control loop can be approximated by combining three fairly straightforward building-block lags. Although these lags may not be precisely representative of the actual system, they are usually similar enough. More seasoned practitioners may utilize other building-block lags, but such requirements are rare and will not be examined in this discussion.

In the typical control loop, lags act in series, the output of one being the input to another. For instance, the lags around a simple temperature loop might be:

The output of a controller is the input to a pneumatic transmission lag.
The output of this transmission lag is the input to a valve lag.
The output of the valve lag is the input to a process heat lag.
The output of the process heat lag is the input to a measurement lag.
The output of the measurement lag is the input to a transmission lag.
The output of the transmission lag is the input to a controller lag.

In this scenario, six lags have been identified, each of which is highly complex if scrutinized in detail. Their cumulative sequential effect can be approximated using two or three basic building-block lags. This is the first point. The second point is that the sequence of the lags or building blocks is inconsequential as long as intermediate points are not of interest. Figure 4.1a illustrates a signal-flow diagram, and Figure 4.1b shows the lags in a jumbled order, which does not make physical sense but yields the same overall lag time, regardless of the order.

Figure 4.1 [For the overall lag, it doesn’t matter whether the component lags are in their proper sequence or scrambled.]

It is important to note that there are two types of lags in real-life systems: interacting and noninteracting lags. Noninteracting lags can be scrambled in order without affecting the overall dynamic behavior of the system, as long as the intermediate points are not of interest. However, this does not apply to interacting lags, where the lag of each element cannot be treated independently since they interact with each other. An example of interacting lags is shown in Figure 4.2, where the level in the second tank affects the flow out of the first. While it may be an academic point at this stage of the development, it is essential to understand the distinction between interacting and noninteracting lags in control systems. Simply taking the lag of each element individually and assuming they act like separate elements is not accurate for interacting lags.

The following names are given to the three types of lags that may be combined to represent most physical systems.

Dead Time
Integrator
First order lag

Figures 4.3 to 4.5 have been included to demonstrate the step response of each type of lag. Let me explain how each behaves when it is part of a closed loop, including the amount of phase lag it introduces and how it impacts the amplitude of the sine wave passing through it.

Figure 4.2 [Interacting lags must be treated as a set of inseparable lags.]

In the upcoming math and algebra sections, the Laplace transforms of these lags will be introduced, providing formulas for phase and amplitude ratios. While these formulas can be used to solve specific problems, most people primarily use them as a type of algebraic shorthand in their work without delving into the more fundamental derivations. Regardless, understanding these concepts is crucial for gaining a deeper understanding of control systems.

Dead Time

Figure 4.3 graphically represents the step response of the dead time lag. This type of lag occurs when an input or cause is applied, but nothing happens until a certain amount of time, known as the dead time, has passed. After the dead time has elapsed, the output is the same as the input. This type of lag is typically associated with the transfer of material or energy between physical locations and is sometimes referred to as a transportation or distance-velocity lag. For example, a coating applied to a film may require downstream thickness measurement.

Different adjectives are often used to distinguish between this type of lag and others that have a similar effect on control. A “pure” dead time refers to this specific type of lag, while other lags may be referred to as “apparent” or “effective” dead time. This distinction is important not only for mathematical and grammatical accuracy but also to convey the relevant information. Later on, you will learn that several of the lags discussed may combine to create a dead time effect in the loop, but they are referred to as apparent dead time.

If the input to a dead time lag is a sine wave, the output will be a sine wave of the same amplitude, for all input periods. The dead time does not filter or dampen any input, but simply delays it. The phase of the output wave lags that of the input wave by:

(1) $\begin{equation*}\frac{360L}{P}\end{equation*}$

degrees. This makes reasoned sense. When $L$ and $P$ match, the phase lag is one full cycle, or $360^{\circ}$ .

Figure 4.3 [With a dead time lag the output follows the input exactly, but delayed by the dead time.]

Math / Algebra

The Laplace transform for a dead time, is:

(2) $\begin{equation*}e^{-Ls}\end{equation*}$

where e is 2.72, the base of the natural logarithms. It is a characteristic of the Laplace transform that you may substitute for s as follows:

(3) $\begin{equation*} s = j\omega\end{equation*}$

(4) $\begin{equation*} \omega = 2 \pi f = 6.28 / P \end{equation*}$

to get the frequency or period response, where

$\omega$ = (omega) = angular frequency

$\pi$ = pi = 3.14

$f$ = frequency = $1 / P$

$L$ = dead time

$P$ = period

Performing a substitution, especially for the dead time, is not desirable, particularly in computer solutions. This is because dead time is usually handled through simulation rather than solving the Laplace transform. Nonetheless, the transform remains a valuable form of notation to convey the topic at hand. The substitution is more beneficial for other types of lags than for dead time.

Integrator

The step response of an integrator or integrating lag is demonstrated in Figure 4.4, which shows that a loop with an integrator can be represented by a level control with a positive displacement pump on either inflow or outflow.

The integrator is essentially the opposite of a dead time lag. It always exhibits a phase lag of $90^{\circ}$ , regardless of the period of oscillation. This was demonstrated in figure 3.5. It’s important to note that while the output of a dead time matched the input at all periods, the output of an integrator does not. Rather, it increases as the period gets longer, which is logical as there is more time for the integration process to take effect.

Figure 4.4 [An integrator lag responds to a step input by a ramp output.]

Math / Algebra

The Laplace transform for the integrator is:

(5) $\begin{equation*} \frac{1}{T_{s}} \end{equation*}$

After substituting for s the amplitude ration is:

(6) $\begin{equation*} \frac{P}{6.28T} \end{equation*}$

As just stated, the longer the period the more time there is to integrate the input wave, so the amplitude is proportional to period. The longer the integrator’s time parameter the slower it is to respond, so the amplitude ratio is inversely proportional to it.

First Order Lag

This next lag is referred to by various names, such as time constant lag, RC lag, exponential lag, simple linear lag, among others. For the sake of consistency, I will refer to it as a first order lag. The name is somewhat arbitrary, but it has gained popularity, and the differential equation that describes it is first order. Figure 4.5 shows its step response.

The slope of the first order lag at any point is such that it would reach the final value in a time known as the time constant. It goes 63% of the way to the final value in one time constant, 95% in three time constants, and 99% in five time constants. This characteristic holds at any point on the curve. If it had gone 23% of the way, it would go 63% of the remaining distance in one time constant. The first order lag results from a resistance of energy or material flow and a storage for that energy or material. For example, the temperature in a stirred tank may respond to a change in wall temperature through a first order lag.

Figure 4.5 [A first order lag will respond exponentially to a step input change.]

The first order lag can be seen as a combination of the pure dead time and the integrator. Its response to a sinusoidal input varies depending on the period of the oscillation in relation to its time constant. If the period is short compared to the time constant, then the phase lag and amplitude ratio will follow the same formula as the integrator. If the period is long compared to the time constant, then it will approach the phase lag and amplitude ratio of a dead time. While this may be plausible by logical reasoning, it is not as straightforward as the dead time and integrator cases.

Math / Algebra

The frequency response of the first order lag is the most complicated of the three simple building blocks. Both the amplitude ratio and the phase lag depend on the period. The Laplace transform is:

(7) $\begin{equation*} \frac{1}{Ts+1} \end{equation*}$

The amplitude ratio is:

(8) $\begin{equation*} \frac{1}{\sqrt{1 + (\omega T)^{2}}} = \frac{1}{\sqrt{1 + (\frac{6.28T}{P})^{2}}} \end{equation*}$

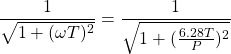
The phase lag:

Phase lag = $\mathrm{tan}^{-1}(\omega T) = \mathrm{tan}^{-1}(\frac{1}{\sqrt{1 + (\frac{6.28T}{P})}})$

The notation “ $\mathrm{tan}^{-1}$ ” is read as the “the angle whose tangent is”. These are complicated and people don’t solve them by hand. If you decide to learn more about frequency response techniques, you will soon memorize these characteristics. They are commonly presented in plots called Bode plots, which will not be presented in this book.

Look at the Laplace transform. When Ts in the denominator is large relative to one, then the denominator is essentially $Ts$ , which makes the transform the same as that for the integrator. Now again, look at the denominator of the transfer function. When $Ts$ is small relative to one, then the transform approaches one.

When $Ts$ is one (when $2 \pi T / P$ is one), the amplitude ratio is 0.707 and the phase lag is $45^{o}$ , a condition commonly called the corner frequency, because in
a Bode plot it is where the asymptotes to the low frequency and high frequency characteristics meet.

Combining Building Blocks

Let’s now combine these building-block lags to create an approximation of a real system. While the order of the lags in a loop can be rearranged without changing the overall result, the step response of the system cannot be drawn in any order. In fact, the order in which the step response is drawn is important and will become clear as you learn the method.

Figure 4.6 [The step response of a series of lags may be drawn by combining the individual lags as shown.]

When a process has pure dead time within a set of lags, it is drawn first when constructing the step response of the entire process from left to right. If there is an integrator, it is drawn last. If there is a first order lag that is long relative to the others, it is also drawn last and the integrating line is delayed accordingly. If there is no pure dead time, then the smaller first order lags are summed and drawn first, delaying the integrator or largest first order lag by that amount.

However, if there is no integrator, no real dead time, and no first order lag that is significantly longer than the rest, there is no straightforward rule for determining an apparent dead time that can be used to predict the natural period. Nonetheless, it is known that the step response will be 50 to 63% complete in a time equal to the sum of the time constants, as shown in Figure 4.7. The 50% point is the limit for an infinite series of infinitely small first order lags (pure dead time), and the 63% point is the limit for a single first order lag. This knowledge provides a way to place a limit on the apparent dead time. However, in this case, the natural period is not necessarily equal to four times the apparent dead time, which introduces an approximation in predicting loop performance.

Figure 4.7 [If very little is known about the component lags in a loop, something about the sum of all the lags can be deduced from knowing the response time as shown above.]

An analogy that can help in understanding how lags combine is the behavior of vehicles at a traffic light turning from red to green. Just like how each vehicle responds after the one before it, elements in a control loop also respond to the one preceding it in the loop. Some drivers may react more slowly than others. However, if you are at the end of a long line of vehicles, the rate at which you can accelerate will be the same regardless of whether the slowest driver was first in line, in the middle, or just in front of you.
Now that you have learned how to estimate the apparent dead time from individual lags in a system, you can also estimate the natural period. It’s not even necessary to draw the step response; you can directly calculate the apparent dead time from the estimated lags.

The natural period is determined by the smaller lags and the dead time, which contribute to $L$ . It is also possible to use the concepts presented here in reverse. If the step response of a system is known, it can be analyzed and broken down into simple lag building blocks. It may not be possible to identify all the lag elements, but it is usually possible to identify some that could combine to form the observed pure dead time, effective dead time, or long first-order lag. This reverse analysis can be a helpful troubleshooting technique.

Math / Algebra

At this point, there isn’t much else to mention about the mathematical aspects, except to highlight the resemblance between the first lag and the dead time when the period is significantly longer than the time constant or dead time.

The following table shows these similarities:

If a loop contains either a dead time element or a first order lag element with a time constant of 0.05 times the natural period, the dead time contributes a phase lag of $17.4^{o}$ while the first order lag contributes a phase lag of $18^{o}$ . The amplitude ratio for the dead time is 0.954, and for the first order lag it is 1.0. These values show that when the phase lag at the natural period is less than 20 or 30 degrees, a dead time and a first order lag behave similarly in a loop.

Gains

Earlier, it was mentioned that the controller gain is largely irrelevant. However, there is another type of gain, the process gain, which is important to understand as it directly affects the controller gain. It is essential to have a comprehensive understanding of control loop components, including not only their time parameter but also their amount parameter. This amount parameter is referred to as gain, and each component will have its own units and dimensions.

The concept of gain is straightforward for self-regulating elements. However, it is more complicated for non-self-regulating elements. For instance, if the outflow from a tank is flow controlled, the level responds to an input flow change by integrating the flow difference. This type of tank is still considered to have gain, but it’s challenging to separate the gain from the integrating time.

It’s common for individuals who haven’t been trained to differentiate time from amount to use the wrong word to describe something. For example, they might say something responds faster when it actually responds more or has more gain. In Figure 4.8, there are two first order lags with identical time constants, but one has twice the gain of the other. Someone who doesn’t understand our control language might say that the one with the higher gain responds faster because its initial slope is twice as fast as the other. However, it’s more accurate to say that it responds more, which is a critical distinction.

Figure 4.8 [Two lags may differ only in gain. The untrained person may say that the one with the higher gain responds faster, when it responds more, not faster.]

Gain has two components: steady-state gain and dynamic gain. The steady-state gain is easy to define, but the dynamic gain is frequency-dependent and is the ratio of the output amplitude to the input amplitude when the input is a sinusoidal change. The dynamic gain is often expressed as a fraction of the steady-state gain, and the terms zero-frequency gain and frequency-dependent gain are used to describe the steady-state and dynamic gains, respectively.

Each element in a control loop has a gain at a particular period, and these gains are multiplied together to obtain the loop gain, which is dimensionless. If the loop gain is less than one at the natural period, the loop will usually be stable, except for the runaway process, which is rare. A runaway system has a step response with an ever-increasing slope, as shown in Figure 4.9. While I focus on time response analysis in this section, the terms steady-state or period-independent gain and period-dependent gain are used for clarity.

Figure 4.9 [If the open-loop step response has an ever increasing slope, there are special control considerations that do not follow the simple rules.]

In chapter 2, we briefly discussed the concept of period-dependent and period-independent components, which may not be as important as $P\cong4L$ , but it is still a useful concept to understand. For pure dead time processes, the gain does not vary with the period, and it is possible to calculate the steady-state gain or zero-frequency gain. Knowing the instrument spans, etc., it is also possible to calculate a controller gain that ensures stability ( $K_{C}<1/K_{p}$ ). If it is not stable at that gain, hardware problems are likely. For processes that do not have an integrator, the period-dependent gain of first-order lags can never be greater than the period-independent gain. This makes it useful for troubleshooting flow control systems, as the period-independent gain is relatively easy to calculate and can be used to calculate a conservative controller gain.

It is also helpful to keep in mind the period-dependent and period-independent components of gain when process conditions change. If a loop was well-tuned but then something changed, it is usually not necessary to retune the loop for every condition. Instead, reasoning whether the change might have affected the period-dependent or period-independent gain, or both, can be helpful. For example, if only the valve position changed and the process lags remained the same, then it may only be necessary to adjust the controller’s gain since the period-dependent gain of a valve typically does not change with position, assuming it has a positioner. However, if it is a diaphragm-operated valve without a positioner, the lag may increase as the volume in the top works increases. This level of detail is beyond the scope of this writing.

Math / Algebra

Until now I have been writing the Laplace transform as only the period-dependent part. To be complete they should have been written with the period-dependent part included. This amounts to simply including $K_{p}$ in the transfer function. For the three lags discussed then, their transfer functions become:

(9) $\begin{equation*}K_{p}e^{-Ls}, \mathrm{dead \ time} \end{equation*}$

(10) $\begin{equation*}\frac{K_{p}}{T_{s}}, \mathrm{integrator}\end{equation*}$

(11) $\begin{equation*}\frac{K_{p}}{T_{s}+1}, \mathrm{first \ order \ lag}\end{equation*}$

Without the $K_{p}$ the transfer functions are dimensionless. $T$ and $L$ have dimensions of time, and $s$ has dimensions of reciprocal time, so their product is dimensionless. $K_{p}$ will have dimensions. For the integrator this is important, because at first it looks like one number over another number. Keeping the two parameters helps keep the dimensions straight.

PID.04 / Lags and Gains +

Dead Time

Math / Algebra

Integrator

Math / Algebra

First Order Lag

Math / Algebra

Combining Building Blocks

Math / Algebra

Gains

Math / Algebra