Statistical Power

Type II errors and power

If your study finds no statistically significant difference between two treatments, it does not necessarily mean that the treatment is ineffective. The study may have missed a real effect due to a small sample size or high variability in the data. This is called a Type II error.

To interpret the results of a study that found no significant difference, you should consider the study’s power to detect hypothetical differences, assuming the same standard deviation between the groups. Power is defined as the fraction of experiments that would lead to statistically significant results if the sample size and level of variation were the same as in the study, and the true difference between the population means was as hypothesized. Typically, alpha (the largest P value considered “significant,” often set to 0.05) is used to determine power.

Example of power calculations

Motulsky et al. asked whether people with hypertension (high blood pressure) had altered numbers of α2-adrenergic receptors on their platelets (Clinical Science 64:265-272, 1983). There are many reasons to think that autonomic receptor numbers may be altered in hypertensives. We studied platelets because they are easily accessible from a blood sample. The results are shown here:

After conducting a t test and obtaining a very high P value, we concluded that the number of α2 receptors in the platelets of hypertensives had not been altered. However, the power of the study to detect a difference (if there was one) depends on the actual size of the difference between the means.

If the true difference in means was 50.58, then the study had only a 50% power to detect a statistically significant difference. In other words, if hypertensives had, on average, 51 more receptors per cell, statistically significant differences would be found in only half of studies of this size, and not in the other half. This difference, amounting to about 20% (51/257), is large enough to have a potential physiological impact.

On the other hand, if the true difference was 84 receptors/cell, then the study had a 90% power to detect a statistically significant difference. Such a large difference would be detected in 90% of studies this size, and not in the remaining 10%.

All studies have low power to find small differences and high power to find large differences. However, the investigator must define “low” and “high” within the context of the experiment and determine whether the power was high enough to justify negative results. If the power is too low, the investigator should avoid reaching a firm conclusion until more subjects are included in the study. In general, most investigators aim for 80% or 90% power to detect a difference.

As this study had only a 50% power to detect a 20% difference in receptor number (equivalent to 50 sites per platelet and large enough to potentially explain certain aspects of hypertension physiology), the negative conclusion cannot be considered definitive.

A Bayesian perspective on interpreting statistical significance

Suppose you are conducting a drug screening study to determine if drugs lower blood pressure. Based on the expected variability in the data and the smallest difference you care about detecting, you have decided on a sample size for each experiment that has 80% power to detect a significant difference at a P value of less than 0.05. If you repeat the experiment many times, the outcome will depend on the context of the experiment.

Consider three alternative scenarios: In scenario A, you have some knowledge of the pharmacology of the drugs and anticipate that only 10% of the drugs will be effective. In scenario B, you have extensive knowledge of the pharmacology of the drugs and expect that 80% of the drugs will be effective. In scenario C, the drugs are selected at random, and you expect only 1% to be effective in lowering blood pressure.

What happens when you perform 1000 experiments in each of these contexts? The calculations are detailed in pages 143-145 of “Intuitive Biostatistics” by Harvey Motulsky (Oxford University Press, 1995). With 80% power, you expect 80% of truly effective drugs to yield a P value less than 0.05. Since you set the definition of statistical significance to 0.05, you expect 5% of ineffective drugs to yield a P value less than 0.05. The outcome of these calculations is shown in tables that are provided in the book.

A. Prior probability=10%

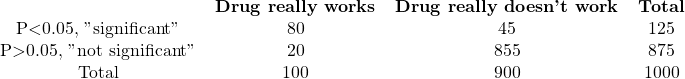
B. Prior probability=80%

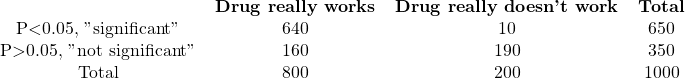
C. Prior probability=1%

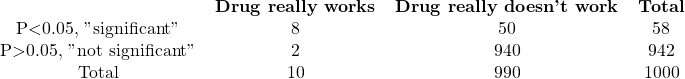
The totals displayed at the bottom of each column depend on the prior probability, which is the specific context of the experiment. The prior probability is equivalent to the proportion of experiments in the leftmost column. To determine the number of experiments in each row, you need to apply the definitions of power and alpha. Not all effective drugs will produce a P value less than 0.05 in every experiment because the chosen sample size was designed to achieve an 80% power. Therefore, 80% of effective drugs will generate a “significant” P value, while the remaining 20% will produce a “not significant” P value. On the other hand, for inactive drugs (middle column), not all experiments will lead to “not significant” outcomes. By setting the definition of statistical significance to “P<0.05” (alpha=0.05), you can expect to observe a significant result in 5% of experiments performed with inactive drugs, while the other 95% will show a “not significant” outcome.

If the P value is less than 0.05, so the results are “statistically significant”, what is the chance that the drug is, in fact, active? The answer is different for each experiment.

The chance of a drug being truly active in experiment A is 64%, calculated as 80/125. If you observe a statistically significant result, there is a 64% chance that the difference is real, while a 36% chance that it occurred randomly. For experiment B, there is a high probability of 98.5% that the difference is real, while in experiment C, there is only a 14% chance that the observed difference is genuine, with an 86% chance of it arising randomly. In other words, most “significant” results in experiment C are due to chance.

Thus, the interpretation of a “statistically significant” result depends on the experiment’s context and cannot be done in isolation. It requires common sense, intuition, and judgment.

Beware of multiple comparisons

Interpreting a single P value is straightforward. Assuming the null hypothesis to be true, the P value indicates the probability of observing a difference in sample means, correlation or association as large as the one obtained in your study, purely by chance due to random subject selection. In other words, if the null hypothesis is true, there is a 5% chance that you will incorrectly infer a treatment effect in the population based on the difference observed between samples.

However, many scientific studies produce multiple P values, and interpreting them can be challenging. If you test several independent null hypotheses and maintain a threshold of 0.05 for each comparison, there is a greater than 5% chance of obtaining at least one “statistically significant” result by chance. The second column of the table below indicates how much higher this probability can be.

Interpreting a single P value is straightforward: assuming the null hypothesis is true, the P value is the probability that random subject selection alone would produce a difference in sample means, correlation, or association at least as significant as that observed in the study. In other words, if the null hypothesis is true, there is a 5% chance of selecting subjects randomly, resulting in a false inference of a treatment effect in the population based on the difference observed between samples.

However, interpreting multiple P values generated by scientific studies can be challenging. If several independent null hypotheses are tested, and the threshold for each comparison is left at 0.05, there is a higher than 5% chance of obtaining at least one “statistically significant” result by chance alone. To maintain the chance of randomly obtaining one statistically significant result at 5%, a stricter (lower) threshold must be set for each individual comparison.

For instance, if you compare control and treated animals and measure the levels of three different enzymes in blood plasma, performing three separate t-tests, one for each enzyme, with a traditional cutoff of alpha=0.05 for declaring each P value to be significant, there is a 14% chance that one or more of your t-tests will be “statistically significant,” even if the treatment has no effect. To reduce the overall chance of a false “significant” conclusion to 5%, the threshold for each t-test needs to be lowered to 0.0170. If ten different enzyme levels are compared with ten t-tests, there is a 40% chance of obtaining at least one “significant” P value by chance alone, even if the treatment has no effect. Failure to correct for multiple comparisons can result in misleading results.

It is only possible to account for multiple comparisons when all the comparisons made by the investigators are known. If only “significant” differences are reported, without disclosing the total number of comparisons, it will be challenging for others to assess the findings. Ideally, all analyses should be planned before data collection, and all results should be reported.

It is necessary to differentiate between studies that test a hypothesis and studies that generate a hypothesis. Exploratory analyses of large databases can generate hundreds of P values, leading to intriguing research hypotheses. It is not possible to test hypotheses using the same data that prompted their consideration. Fresh data must be used to test hypotheses.

If an experiment involves three or more groups, t-tests should not be performed, even if multiple comparisons are corrected. Instead, the data should be analyzed using one-way analysis of variance (ANOVA) followed by post-tests. These methods account for both multiple comparisons and the non-independence of comparisons.