Note that in this section, the language of control systems is employed, which may diverge from the terminology used by engineers in the process industries. Thus, it’s worth noting that when the word “system” is mentioned in this text, it pertains to the process, while “system output” denotes the controlled variable ![]() , “system input” is equivalent to the manipulated variable
, “system input” is equivalent to the manipulated variable ![]() , and “reference signal” signifies the set point in everyday PID terminology.
, and “reference signal” signifies the set point in everyday PID terminology.
Introduction
The conventional control theory and techniques we have covered in class, such as root locus, are based on a straightforward input-output depiction of the plant, typically expressed as a transfer function. These approaches do not incorporate any information about the internal structure of the plant, restricting us to single-input single-output (SISO) systems and providing limited control of the closed-loop behavior when feedback control is employed.
Modern control theory overcomes many of these limitations by employing a much more comprehensive representation of the plant dynamics. The state-space description, also known as the internal model, offers the dynamics as a group of linked first-order differential equations in a set of internal variables called state variables, along with a set of algebraic equations that combine the state variables into physical output variables.
Definition of System State
The state of a dynamic system refers to the minimum set of variables, known as state variables, that fully describe the system and its response to any given set of inputs [1-3]. A state-determined system model is characterized by a mathematical description of the system in terms of a minimum set of variables ![]() , along with knowledge of those variables at an initial time
, along with knowledge of those variables at an initial time ![]() and the system inputs for time
and the system inputs for time ![]() , which are sufficient to predict the future system state and outputs for all time
, which are sufficient to predict the future system state and outputs for all time ![]() .
.
The dynamic behavior of a state-determined system is fully defined by the response of the set of n variables ![]() , where the number
, where the number ![]() is the order of the system. For example, the system shown in Fig. 1 has two inputs
is the order of the system. For example, the system shown in Fig. 1 has two inputs ![]() and
and ![]() and four output variables
and four output variables ![]() . If the system is state-determined, knowledge of its state variables
. If the system is state-determined, knowledge of its state variables ![]() at some initial time
at some initial time ![]() , and the inputs
, and the inputs ![]() and
and ![]() for
for ![]() are sufficient to determine all future behavior of the system. The state variables are an internal description of the system that fully characterize the system state at any time
are sufficient to determine all future behavior of the system. The state variables are an internal description of the system that fully characterize the system state at any time ![]() , from which any output variables
, from which any output variables ![]() can be computed.
can be computed.
State-determined system models can represent large classes of engineering, biological, social, and economic systems. Systems constructed with pure and ideal one-port elements, such as mass, spring, and damper elements, are state-determined system models, where the number of state variables, ![]() , equals the number of independent energy storage elements in the system. The values of the state variables at any time
, equals the number of independent energy storage elements in the system. The values of the state variables at any time ![]() specify the energy of each energy storage element within the system and the total system energy, while the time derivatives of the state variables determine the rate of change of the system energy. Moreover, the values of the system state variables at any time
specify the energy of each energy storage element within the system and the total system energy, while the time derivatives of the state variables determine the rate of change of the system energy. Moreover, the values of the system state variables at any time ![]() provide sufficient information to determine the values of all other variables in the system at that time.
provide sufficient information to determine the values of all other variables in the system at that time.
Although there is no unique set of state variables that describe any given system, for a given system, the order ![]() is unique and independent of the particular set of state variables chosen. State variable descriptions of systems may be formulated in terms of physical and measurable variables or in terms of variables that are not directly measurable. It is possible to mathematically transform one set of state variables to another, as long as any set of state variables provides a complete description of the system. This note focuses on a particular set of state variables based on energy storage variables in physical systems.
is unique and independent of the particular set of state variables chosen. State variable descriptions of systems may be formulated in terms of physical and measurable variables or in terms of variables that are not directly measurable. It is possible to mathematically transform one set of state variables to another, as long as any set of state variables provides a complete description of the system. This note focuses on a particular set of state variables based on energy storage variables in physical systems.
Figure 1.1 [System inputs and outputs].
The State Equations
A standard form for the state equations is used throughout system dynamics. In the standard form the mathematical description of the system is expressed as a set of n coupled first-order ordinary differential equations, known as the state equations, in which the time derivative of each state variable is expressed in terms of the state variables ![]() and the system
and the system
inputs ![]() . In the general case the form of the n state equations is:
. In the general case the form of the n state equations is:
(1) 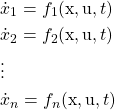
where ![]() and each of the functions
and each of the functions ![]() may be a general nonlinear, time varying function of the state variables, the system inputs, and time.
may be a general nonlinear, time varying function of the state variables, the system inputs, and time.
It is common to express the state equations in a vector form, in which the set of n state variables is written as a state vector ![]() , and the set of
, and the set of ![]() inputs is written as an input vector
inputs is written as an input vector ![]() . Each state variable is a time varying component of the column vector
. Each state variable is a time varying component of the column vector ![]() .
.
This form of the state equations explicitly represents the basic elements contained in the definition of a state determined system. Given a set of initial conditions (the values of the ![]() at some time
at some time ![]() ) and the inputs for
) and the inputs for ![]() , the state equations explicitly specify the derivatives of all state variables. The value of each state variable at some time
, the state equations explicitly specify the derivatives of all state variables. The value of each state variable at some time ![]() later may then be found by direct integration.
later may then be found by direct integration.
The system state at any instant may be interpreted as a point in an n-dimensional state space, and the dynamic state response ![]() can be interpreted as a path or trajectory traced out in the state space.
can be interpreted as a path or trajectory traced out in the state space.
In vector notation the set of n equations in Eqs. (1) may be written:
(2) ![]()
where ![]() is a
is a ![]() function with
function with ![]() components
components ![]() .
.
In this note we restrict attention primarily to a description of systems that are linear and time-invariant (LTI), that is systems described by linear differential equations with constant coefficients. For an LTI system of order ![]() , and with
, and with ![]() inputs, Eqs. (1) become a set of
inputs, Eqs. (1) become a set of ![]() coupled first-order linear differential equations with constant coefficients:
coupled first-order linear differential equations with constant coefficients:
(3) 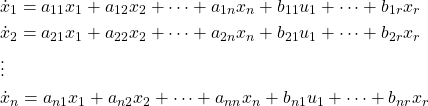
where the coefficients ![]() and
and ![]() are constants that describe the system. This set of
are constants that describe the system. This set of ![]() equations defines the derivatives of the state variables to be a weighted sum of the state variables and the system inputs.
equations defines the derivatives of the state variables to be a weighted sum of the state variables and the system inputs.
Equations (8) may be written compactly in a matrix form:
(4) 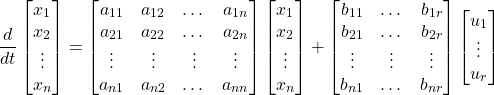
which may be summarised as:
(5) ![]()
where the state vector ![]() is a column vector of length
is a column vector of length ![]() , the input vector
, the input vector ![]() is a column vector of length
is a column vector of length ![]() ,
, ![]() is an
is an ![]() square matrix of the constant coefficients
square matrix of the constant coefficients ![]() , and
, and ![]() is an
is an ![]() matrix of the coefficients
matrix of the coefficients ![]() that weight the inputs.
that weight the inputs.
Output Equations
A system output is defined to be any system variable of interest. A description of a physical system in terms of a set of state variables does not necessarily include all of the variables of direct engineering interest. An important property of the linear state equation description is that all system variables may be represented by a linear combination of the state variables ![]() and the system inputs
and the system inputs ![]() . An arbitrary output variable in a system of order
. An arbitrary output variable in a system of order ![]() with
with ![]() inputs may be written:
inputs may be written:
(6) ![]()
where the ![]() and
and ![]() are constants. If a total of
are constants. If a total of ![]() system variables are defined as outputs, the
system variables are defined as outputs, the ![]() such equations may be written as:
such equations may be written as:
(7) 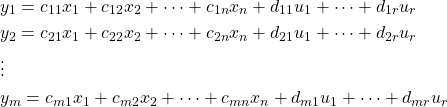
or in matrix form:
(8) 
The output equations, Eqs. (8), are commonly written in the compact form:
(9) ![]()
where ![]() is a column vector of the output variables
is a column vector of the output variables ![]() ,
, ![]() is an
is an ![]() matrix of the constant coefficients
matrix of the constant coefficients ![]() that weight the state variables, and
that weight the state variables, and ![]() is an
is an ![]() matrix of the constant coefficients
matrix of the constant coefficients ![]() that weight the system inputs. For many physical systems the matrix
that weight the system inputs. For many physical systems the matrix ![]() is the null matrix, and the output equation reduces to a simple weighted combination of the state variables:
is the null matrix, and the output equation reduces to a simple weighted combination of the state variables:
(10) ![]()
State Equation Based Modelling Procedure
The complete system model for a linear time-invariant system consists of (i) a set of ![]() state equations, defined in terms of the matrices
state equations, defined in terms of the matrices ![]() and
and ![]() , and (ii) a set of output equations that relate any output variables of interest to the state variables and inputs, and expressed in terms of the
, and (ii) a set of output equations that relate any output variables of interest to the state variables and inputs, and expressed in terms of the ![]() and
and ![]() matrices. The task of modelling the system is to derive the elements of the matrices, and to write the system model in the form:
matrices. The task of modelling the system is to derive the elements of the matrices, and to write the system model in the form:
(11) ![]()
(12) ![]()
The matrices ![]() and
and ![]() are properties of the system and are determined by the system structure and elements. The output equation matrices
are properties of the system and are determined by the system structure and elements. The output equation matrices ![]() and
and ![]() are determined by the particular choice of output variables.
are determined by the particular choice of output variables.
The overall modelling procedure developed in this chapter is based on the following steps:
- Determination of the system order n and selection of a set of state variables from the linear graph system representation.
- Generation of a set of state equations and the system A and B matrices using a well defined methodology. This step is also based on the linear graph system description.
- Determination of a suitable set of output equations and derivation of the appropriate C and D matrices.
