A multiple-input multiple-output system is written in terms of the ![]() component input vector
component input vector ![]()
(1) ![]()
generating a set of ![]() simultaneous linear equations, where the matrix
simultaneous linear equations, where the matrix ![]() is
is ![]() . The
. The ![]() component system output vector
component system output vector ![]() may be found by substituting this solution for
may be found by substituting this solution for ![]() into the output equation as in Eq. 2:
into the output equation as in Eq. 2:
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} & \mathrm{Y}(s) = \mathrm{C}[s \mathrm{I} - \mathrm{A}]^{-1}\mathrm{B}\{\mathrm{U}(s)\} + \mathrm{D}\{\mathrm{U}(s)\} \\ & \mathrm{Y}(s) = [\mathrm{C}[s \mathrm{I} - \mathrm{A}]^{-1}\mathrm{B} + \mathrm{D}]\{\mathrm{U}(s)\} \end{split} \end{equation*}](http://prizm.studio/wp-content/ql-cache/quicklatex.com-d90787bbab1305461357eebefcfdcb5f_l3.png)
and expanding the inverse in terms of the determinant and the adjoint matrix
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} & \mathrm{Y}(s) = \frac{\mathrm{C} \; \mathrm{adj}(s\mathrm{I} - \mathrm{A}) \mathrm{B} + \mathrm{det} [s \mathrm{I} - \mathrm{A}] \mathrm{D}}{\mathrm{det}[s \mathrm{I} - \mathrm{A}] \mathrm{D}} \mathrm{U}(s) \\ & \mathrm{Y}(s) = \mathrm{H}(s)\mathrm{U}(s) \end{split} \end{equation*}](http://prizm.studio/wp-content/ql-cache/quicklatex.com-e3d50da1789046696775d44d2e5830a7_l3.png)
where ![]() is defined to be the matrix transfer function relating the output vector
is defined to be the matrix transfer function relating the output vector ![]() to the input vector
to the input vector ![]() :
:
(4) ![]()
For a system with ![]() inputs
inputs ![]() and
and ![]() outputs
outputs ![]() is a
is a ![]() matrix whose elements are individual scalar transfer functions relating a given component of the output
matrix whose elements are individual scalar transfer functions relating a given component of the output ![]() to a component of the input
to a component of the input ![]() . Expansion of Eq. 3 generates a set of equations:
. Expansion of Eq. 3 generates a set of equations:
(5) 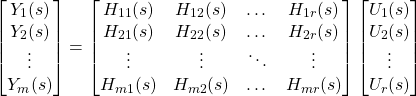
where the ![]() th component of the output vector
th component of the output vector ![]() is:
is:
(6) ![]()
The elemental transfer function ![]() is the scalar transfer function between the
is the scalar transfer function between the ![]() thoutput component and the
thoutput component and the ![]() th input component. Equation 5 shows that all of the
th input component. Equation 5 shows that all of the ![]() transfer functions in
transfer functions in ![]() have the same denominator factor
have the same denominator factor ![]() , giving the important result that all input-output differential equations for a system have the same characteristic polynomial, or alternatively have the same coefficients on the left-hand side.
, giving the important result that all input-output differential equations for a system have the same characteristic polynomial, or alternatively have the same coefficients on the left-hand side.
If the system has a single-input and a single-output, ![]() is a scalar, and the procedure generates the input/output transfer operator directly.
is a scalar, and the procedure generates the input/output transfer operator directly.