SS.05 / Transformation From State-Space Equations to Classical Form +

The transfer function and the classical input-output differential equation for any system variable may be found directly from a state space representation through the Laplace transform.

The following example illustrates the general method for a first-order system.

Classical representations of higher-order systems may be derived in an analogous set of steps by using the Laplace transform and matrix algebra. A set of linear state and output equations written in standard form:

(1) $\begin{equation*} \dot{\mathrm{x}} = \mathrm{Ax} + \mathrm{Bu} \end{equation*}$

(2) $\begin{equation*} \mathrm{y} = \mathrm{Cx} + \mathrm{Du} \end{equation*}$

may be rewritten in the Laplace domain. The system equations are then

(3) $\begin{equation*} \begin{split} & s\mathrm{X}(s) = \mathrm{A}X(s) + \mathrm{B}U(s) \\ & \mathrm{Y}(s) = \mathrm{CX}(s) + \mathrm{DU}(s) \end{split} \end{equation*}$

and the state equations may be rewritten:

(4) $\begin{equation*} s\mathrm{x}(s) - \mathrm{Ax}(s) = [s\mathrm{I} - \mathrm{A}] \mathrm{x}(s) = \mathrm{Bu}(s) \end{equation*}$

where the term $s\mathrm{I}$ creates an $n \times n$ matrix with $s$ on the leading diagonal and zeros elsewhere. (This step is necessary because matrix addition and subtraction is only defined for matrices of the same dimension.) The matrix $[s\mathrm{I} \minus \mathrm{A}]$ appears frequently throughout linear system theory; it is a square $n \times n$ matrix with elements directly related to the $\mathrm{A}$ matrix:

(5) $\begin{equation*} [s\mathrm{I} - A] = \begin{bmatrix} (s - a_{11} & - a_{12} & \dots & - a_{1n} \\ - a_{21} & (s - a_{22}) & \dots & - a_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ -a_{n1} & -a_{n2} & \dots & (s - a_{nn}) \end{bmatrix} \end{equation*}$

The state equations, written in the form of Eq. (4), are a set of n simultaneous operational expressions. The common methods of solving linear algebraic equations, for example Gaussian elimination, Cramer’s rule, the matrix inverse, elimination and substitution, may be directly applied to linear operational equations such as Eq. (4).
For low-order single-input single-output systems the transformation to a classical formulation may be performed in the following steps:

Take the Laplace transform of the state equations.
Reorganize each state equation so that all terms in the state variables are on the left-hand side.
Treat the state equations as a set of simultaneous algebraic equations and solve for those state variables required to generate the output variable.
Substitute for the state variables in the output equation.
Write the output equation in operational form and identify the transfer function.
Use the transfer function to write a single differential equation between the output variable and the system input.

Example

Use the Laplace transform method to derive a single differential equation for the capacitor voltage $v_{C}$ in the series R-L-C electric circuit shown in Fig. 1.1.

Figure 1.1 [A series RLC circuit].

Solution: The linear graph method of state equation generation selects the capacitor voltage $v_{C}(t)$ and the inductor current $i_{L}(t)$ as state variables, and generates the following pair of state equations:

(6) $\begin{equation*} \begin{bmatrix} \dot{v}_c \\ \dot{i}_{L} \end{bmatrix} = \begin{bmatrix} 0 & 1/C \\ -1/L & -R/L \end{bmatrix} \begin{bmatrix} v_{c} \\ i_{L}\end{bmatrix} + \begin{bmatrix} 0 \\ 1/L \end{bmatrix} V_{in} \end{equation*}$

The required output equation is:

(7) $\begin{equation*} y(t) = \begin{bmatrix} 0 & 1 \end{bmatrix} \begin{bmatrix} v_{c} \\ i_{L}\end{bmatrix} + \begin{bmatrix} 0 \end{bmatrix} V_{in} \end{equation*}$

Step 1: In Laplace transform form the state equations are:

(8) $\begin{equation*} & sV_{C}(s) = 0V_{C}(s) + 1/CI_{L}(s) + 0V_{s}(s) \end{equation*}$

(9) $\begin{equation*} & sI_{L}(s) = -1/LV_{C}(s) - R/LI_{L}(s) + 1/LV_{s}(s) \end{equation*}$

Step 2: Reorganize the state equations:

(10) $\begin{equation*} & sV_{C}(s) - 1/CI_{L}(s) = 0V_{s}(s) \end{equation*}$

(11) $\begin{equation*} & 1/LV_{C}(s) + [s + R/L]I_{L}(s) = 1/LV_{s}(s) \end{equation*}$

Step 3: In this case we have two simultaneous operational equations in the state variables $v_{C}$ and $i_{L}$ . The output equation requires only $v_{C}$ . If Eq. (iv) is multiplied by $[s + R/L]$ , and Eq. (v) is multiplied by $1/C$ , and the equations added, $I_{L}(s)$ is eliminated:

(12) $\begin{equation*} [s(s + R/L) + 1/LC] V_{C}(s) = 1/LCV_{s}(s) \end{equation*}$

Step 4: The output equation is $y = v_{C}$ . Operate on both sides of Eq. (12) by $[s^{2} + (R/L)s + 1/LC]^{−1}$ and write in quotient form:

(13) $\begin{equation*} V_{C}(s) = \frac{1/LC}{s^{2} + (R/L)s + 1/LC} V_{s}(s) \end{equation*}$

Step 5: The transfer function $H(s) = V_{c}(s)/V_{s}(s)$ is:

(14) $\begin{equation*} H(s) = \frac{1/LC}{s^{2} + (R/L)s + 1/LC} \end{equation*}$

Step 6: The differential equation relating $v_{C}$ to $V_{s}$ is:

(15) $\begin{equation*} \frac{d^{2}v_{C}}{dt^{2}} + \frac{R}{L} \frac{dv_{C}}{dt} + \frac{1}{LC}v_{C} = \frac{1}{LC}V_{s}(t) \end{equation*}$

Cramer’s Rule, for the solution of a set of linear algebraic equations, is a useful method to apply to the solution of these equations. In solving for the variable $x_{i}$ in a set of $n$ linear algebraic equations, such as $\mathrm{Ax} = \mathrm{b}$ the rule states:

(16) $\begin{equation*} x_{i} = \frac{\mathrm{det}[\mathrm{A}^{(i)}]}{det[\mathrm{A}]} \end{equation*}$

where $\mathrm{A}^{(i)}$ is another $n × n$ matrix formed by replacing the $i$ th column of $\mathrm{A}$ with the vector $\mathrm{b}$ .
If

(17) $\begin{equation*} [s\mathrm{I} - \mathrm{A}]\mathrm{X}(s) = \mathrm{BU}(s) \end{equation*}$

then the relationship between the $i$ th state variable and the input is

(18) $\begin{equation*} X_{i}(s) = \frac{\mathrm{det}[[s\mathrm{I} - \mathrm{A}]^{(i)}]}{\mathrm{det}[s\mathrm{I} - \mathrm{A}]} U(s) \end{equation*}$

where $(s\mathrm{I} − \mathrm{A})^{(i)}$ is defined to be the matrix formed by replacing the $i$ th column of $(s\mathrm{I} − \mathrm{A})$ with the column vector $\mathrm{A}$ . The differential equation is

(19) $\begin{equation*} \mathrm{det}[s\mathrm{I} - \mathrm{A}] x_{i} = \mathrm{det}[(s\mathrm{I} - \mathrm{A})^{(i)}] u_{k}(t) \end{equation*}$

Example

Use Cramer’s Rule to solve for $v_{L}(t)$ in the electrical system of the previous example.

Solution: From the previous example, the state equations are:

(20) $\begin{equation*} \begin{bmatrix} \dot{v}_c \\ \dot{i}_{L} \end{bmatrix} = \begin{bmatrix} 0 & 1/C \\ -1/L & -R/L \end{bmatrix} \begin{bmatrix} v_{c} \\ i_{L}\end{bmatrix} + \begin{bmatrix} 0 \\ 1/L \end{bmatrix} V_{in} \end{equation*}$

and the output equation is:

(21) $\begin{equation*} v_{L} = -v_{C} - Ri_{L} + V_{s}(t). \end{equation*}$

In the Laplace domain the state equations are:

(22) $\begin{equation*} \begin{bmatrix} s & -1/C \\ 1/L & s + R/L \end{bmatrix} + \begin{bmatrix} V_{C}(s) \\ I_{L}(s) \end{bmatrix} = \begin{bmatrix} 0 \\ I/L \end{bmatrix} V_{in}(s). \end{equation*}$

The voltage $V_{C}(s)$ is given by:

(23) $\begin{equation*} \begin{split} & V_{C}(s) = \frac{\mathrm{det}[(s\mathrm{I} - \mathrm{A})^{(1)}]}{\mathrm{det}[(s\mathrm{I} - \mathrm{A})]} V_{in}(s) \\ & V_{C}(s) = \frac{\mathrm{det}\begin{bmatrix} 0 & -1/C \\ 1/L & (s + R/L)\end{bmatrix}}{\mathrm{det}\begin{bmatrix} s & -1/C \\ 1/L & (s + R/L)\end{bmatrix}} V_{in}(s) \\ & V_{C}(s) = \frac{1/LC}{s^{2} + (R/L)s + (1/LC)} V_{in}(s) \end{split} \end{equation*}$

The current $I_{L}(t)$ is:

(24) $\begin{equation*} \begin{split} & I_{L}(s) = \frac{\mathrm{det}[(s\mathrm{I} - \mathrm{A})^{(2)}]}{\mathrm{det}[(s\mathrm{I} - \mathrm{A})]} V_{in}(s) \\ & I_{L}(s) = \frac{\mathrm{det}\begin{bmatrix} s & 0 \\ 1/L & 1/L\end{bmatrix}}{\mathrm{det}\begin{bmatrix} s & -1/C \\ 1/L & (s + R/L)\end{bmatrix}} V_{in}(s) \\ & I_{L}(s) = \frac{s/L}{s^{2} + (R/L)s + (1/LC)} V_{in}(s) \end{split} \end{equation*}$

The output equation may be written directly from the Laplace transform of Eq.(21):

(25) $\begin{equation*} \begin{split} & V_{L}(s) = -V_{C}(s) - RI_{L}(s) + V_{s}(s) \\ & V_{L}(s) = [\frac{-1/LC}{s^{2} + (R/L)s + (1/LC)} + \frac{-(R/L)s}{s^{2} + (R/L)s + (1/LC)} + 1] V_{s}(s) \\ & V_{L}(s) = \frac{-1/LC - (R/L)s + (s^{2} + (R/L)s + (1/LC))}{s^{2} + (R/L)s + (1/LC)} V_{s}(s) \\ & V_{L}(s) = \frac{s^{2}}{s^{2} + (R/L)s + (1/LC)} V_{s}(s) \end{split} \end{equation*}$

giving the differential equation

(26) $\begin{equation*} \frac{d^{2}v_{L}}{dt^{2}} + \frac{R}{L} \frac{dv_{L}}{dt} + \frac{1}{LC} v_{L}(t) = \frac{d^{2}V_{s}}{dt^{2}} \end{equation*}$

For a single-input single-output (SISO) system the transfer function may be found directly by evaluating the inverse matrix

(27) $\begin{equation*} \mathrm{X}(s) = (s \mathrm{I} - \mathrm{A})^{-1} \mathrm{B} U(s). \end{equation*}$

Using the definition of the matrix inverse:

(28) $\begin{equation*} [s \mathrm{I} - \mathrm{A}]^{-1} = \frac{\mathrm{adj}[s \mathrm{I} - \mathrm{A}]}{\mathrm{det}[s \mathrm{I} - \mathrm{A}]} \end{equation*}$

(29) $\begin{equation*} \mathrm{X}(s) = \frac{\mathrm{adj}[s \mathrm{I} - \mathrm{A}] \mathrm{B}}{\mathrm{det}[s \mathrm{I} - \mathrm{A}]} U(s). \end{equation*}$

and substituting into the output equations gives:

(30) $\begin{equation*} \begin{split} & Y(s) = \mathrm{C}[s \mathrm{I} - \mathrm{A}]^{-1} \mathrm{B}U(s) + \mathrm{D}U(s) \\ & Y(s) = [\mathrm{C}[s \mathrm{I} - \mathrm{A}]^{-1} \mathrm{B} + \mathrm{D}] U(s). \end{split} \end{equation*}$

Expanding the inverse in terms of the determinant and the adjoint matrix yields:

(31) $\begin{equation*} \begin{split} & Y(S) = \frac{\mathrm{C} \mathrm{adj} (s \mathrm{I} - \mathrm{A}) \mathrm{B} + \mathrm{det}[s \mathrm{I} - \mathrm{A}] \mathrm{D}}{\mathrm{det}[s \mathrm{I} - \mathrm{A}]} U(s) \\ & Y(S) = H(s)U(s) \end{split} \end{equation*}$

so that the required differential equation may be found by expanding:

(32) $\begin{equation*} \mathrm{det} [s \mathrm{I} - \mathrm{A}] Y(s) = [\mathrm{C} \; \mathrm{adj} (s \mathrm{I} - \mathrm{A}) \mathrm{B} + \mathrm{det}[s \mathrm{I} - \mathrm{A}] \mathrm{D}] U(s). \end{equation*}$

and taking the inverse Laplace transform of both sides.

Example

Use the matrix inverse method to find a differential equation relating $v_{L}(t)$ to $V_{s}(t)$ in the system described in the third example.

Solution: The state vector, written in the Laplace domain,

(33) $\begin{equation*} \mathrm{X}(s) = [s \mathrm{I} - \mathrm{A}]^{-1} \; \mathrm{BU}(s) \end{equation*}$

from the previous example is:

(34) $\begin{equation*} \begin{bmatrix} V_{c}(s) \\ I_{L}(s) \end{bmatrix} = \begin{bmatrix} s & -1/C \\ 1/L & s + R/L \end{bmatrix} ^{-1} \begin{bmatrix} 0 \\ 1/L \end{bmatrix} \; V_{in}(s). \end{equation*}$

The determinant of $[s \mathrm{I} − \mathrm{A}]$ is

(35) $\begin{equation*} \mathrm{det} [s \mathrm{I} - \mathrm{A}] = (s^{2} + (R/L)s + (1/LC)) \end{equation*}$

and the adjoint of $[s \mathrm{I} − \mathrm{A}]$ is

(36) $\begin{equation*} \mathrm{adj} \begin{bmatrix} s & -1/C \\ 1/L & s + R/L \end{bmatrix} = \begin{bmatrix} s+ R/L & 1/C \\ -1/L & s \end{bmatrix}. \end{equation*}$

From the current and the previous example, the output equation $v_{L}(t) = −v_{C} − Ri_{L} + V_{s}(t)$ specifies that $\mathrm{C} = [−1 − R]$ and $\mathrm{D} = [1]$ . The transfer function, Eq. (26) is:

(37) $\begin{equation*} H(s) = \frac{\mathrm{C}\; \mathrm{adj} (s \mathrm{I} - \mathrm{A}) \mathrm{B} + \mathrm{det}[s \mathrm{I} - \mathrm{A}] \; \mathrm{D}}{\mathrm{det} [s \mathrm{I} - \mathrm{A}]^{-1}}. \end{equation*}$

Since

(38) $\begin{equation*} \begin{split} & \mathrm{C} \; \mathrm{adj} (s \mathrm{I} - \mathrm{A}) \mathrm{B} = \begin{bmatrix} -1 & -R \end{bmatrix} \begin{bmatrix} s + R/L & 1/C \\ -1/L & s \end{bmatrix} \begin{bmatrix} 0 \\ 1/L \end{bmatrix} \\ & \mathrm{C} \; \mathrm{adj} (s \mathrm{I} - \mathrm{A}) \mathrm{B} = - \frac{R}{L}s - \frac{1}{LC}, \end{split} \end{equation*}$

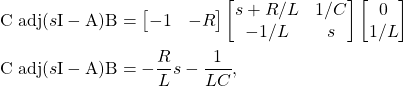
the transfer function is

(39) $\begin{equation*} \begin{split} & H(s) = \frac{-(R/L)s - 1/(LC) + (s^{2} + (R/L)s + (1/LC)) \begin{bmatrix} 1 \end{bmatrix}}{(s^{2} + (R/L)s + (1/LC))} \\ & H(s) = \frac{s^{2}}{(S^{2} + (R/L)S + (1/LC))}, \end{split} \end{equation*}$

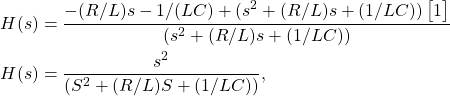
which is the same result found by using Cramer’s rule in the previous example.